Differences between viewing a
3D scene and a pair of 2D pictures
The question is of course how depth is experienced when
using a stereo pair and how this relates to the depth
experience of the actual 3D scene. At this moment, I
recognize three types of situations (
again following the work
flow from real experience to picture taking to observing 2D
pictures):
- normal viewing of a 3D scene with two eyes.
- making a stereo pair with two lenses
- viewing a stereo pair with the eyes
(A and C are of course the most important ones as these are
the human experiences; B is just a step to get to C).
These three have quiet different properties (below is
concentrating on still stereo photography, I can understand
it might be different for stereo video). In the below
fixation distance (for
eyes) with
vergence
distance (for a camera lenses) are somewhat
equivalent terms:
- Variable focused distance, small eye Depth of Field
(DoF), linked (with focused distance) fixation distance:
- The focused distance and fixation distance are
(normally) the same/liked.
- The eye DoF is quite small in most (all) situations.
- The fixation distance normally represents a
convergence angle (positive fixation distance)
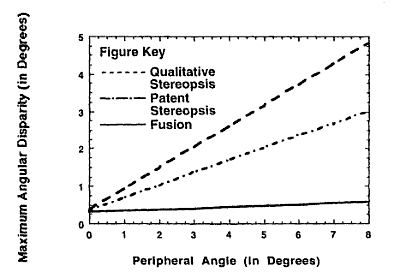
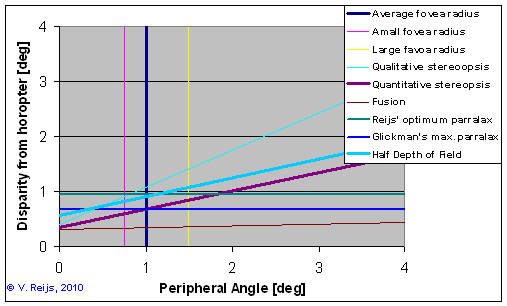
- The range where a human can experience depth is
quite small: patent/quantitative stereopsis (without changing the eye's
fixation distance [aka horopter distance]).
It is interesting to see that the eye DoF range is
quite comparable to the
patent stereopsis range (perhaps obvious when knowing
evolution theory;-) Also important is that the
eye/brain combination rejects things outside quantitative
stereopsis (it makes them almost invisible).
- The stereo window distance (zero deviation) is
normally at the fixation distance (as the eye needs to
put the deviation at zero at that location to make
proper interpretations by the brain possible).
- There is thus a lot of window violation (everything
in front of the fixation is closer then the fixation
distance aka window distance,) luckily the window itself is
very blurry with our eyes!
- The eyes have to scan over the whole scene (using
different focused/fixations distance) to get the full
scene.
- Camera looking at the whole scene: fixed focused
distance, large camera DoF, fixed vergence distance
- The focused distance is fixed at a point which the
photographer finds the most interesting.
- In stereo photography it seems we choice a large
camera DoF (to allow to see a deep scene).
Would DoF in
video be smaller than in still photography?
- The vergence distance normally represents a
convergence angle (positive vergence distance), but it
can be also divergence angle (negative vergence
distance).
Would vergence
distance be the same as the focused distance for
stereo video? See also this
video
of the converging lenses for Cameron's film Avatar.
- As the camera DoF is large the focused distance is
not that important
- The stereo window distance (zero deviation) is (by
default) at the vergence distance.
- No scanning of camera lenses possible over the scene
(so it stays a fixed focused/vergence).
- Fixed focused distance, small eye DoF, variable
fixation distance
- As the focus distance is the distance to the screen,
every thing on that screen is in focus. As the camera
DoF of the 2D picture was large, the eye sees much
more sharp than in real live.
- The small eye DoF is not important here as the 2D
picture are all in one plane
- The fixation distance normally represents a
convergence angle (positive vergence distance), but it
can be also divergence angle (negative vergence
distance)
- As the eye sees much more sharp, this causes the
strain on the eyes (more conflicts are explicitly
visible, while not really visible with the real 3D
scene). The eye/brain combination has more difficulty
in rejecting
non fusible parts of the scene (like with far/near
objects, where keystoning distortions might have
happened in step B due to con/divergence), as the
camera's DoF was large.
- Further more the focus and the fixation distance are
different (not linked), and thus also not really as
humans are used to in real live.
- The stereo window distance is determined by the two
2D pictures' relative shift.
- The eyes have to scan over the whole scene (using
constant focused but different fixation distance) to
get the full scene.
With video the
eyes don't really have time to wander?
So there are a few difference between these situations A and
C. I think that these difference (and a few others: like
motion parallax) can quiet well explain the issues around
stereo viewing. Some (all?) of these differences might
explain the
stress in the eyes
in certain cases.
Here are some differences made more explicit when looking at
a real 3D scene and using a stereo pair:
- different retinal disparity. For instance in 3D scene
one's eyes fixate/converge on the object and this will
change the angle one sees the background (Glickman, B.,
pers. comm. [2009]), this change in angle is not
experienced in a static stereo pair)
- the viewer's accommodation/focus is not depending on
the depth in the 3D scene when looking at the 2D
pictures
- focus areas of 2D pictures are fixed, while this
is variable with eyes looking in the 3D scene.
- the brain can block parts of the scene that have too
much disparity: only one eye image is used. This is not
happening when admiring a stereo pair (with video less a
problem due to less attention to main object).
- motion parallax is present with 3D scene as a human's
head is never static (not the case for in static stereo
pair, although if one moves one's head slightly with a
stereo pair, the impression of motion parallax is
there).
- no motion parallax in stereo pair when converging eyes
to a certain part in the pair (present when looking at
3D scene).
- Scanning the scene by the eyes does not result in
changes of stereo pair experience, but it would happen
with a 3D scene.
- there could be misalignments due to bad stereo picture
taking (like rotation,
vertical misalignment, size, pincushion/barrel
distortion, etc.)
- difference due to the presentation method used for the
stereo viewing method.(key stoning with cross viewing,
color changes with anaglyphs, etc.)
- different 3D image experience due to hard picture
boundaries (stereo window or the size patent stereopsis)
- different importances of
cues/constancies when viewing a pair, see below
- etc.? Let me know.
Three types of 3D images when
looking at a stereo pairs
The following types of 3D images (as perceived in the brain)
can be
seen by a
viewer of a stereo pair (and one can switch between them by
proper attention/concentration of the viewer). These types
are proposed by the author of these pages.
This section is at this moment primarily about cross free
viewing (as I personally can experience type 1 and type 2),
but should work for any viewing method (will be updated in
the future).
Type 1: Geometric 3D image
When cross viewing, the geometric 3D image can be seen
between the screen and the eyes. It is based on the geometry
of the eye locations and the homologous points on the 2D
pictures. The convergence/accommodation (oculomotor) cue is
important here. This type might be a form of proximal mode
(see Rock, [
1995],
page 44 and 45).
See in below picture of cross free viewing:
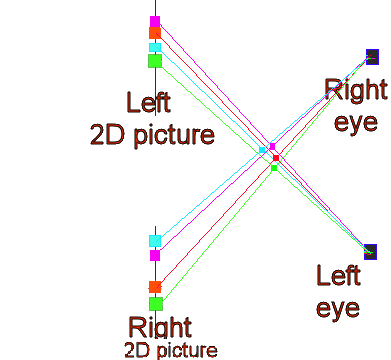 Cross free viewing
Cross free viewing
When just learning cross
free viewing, this was the way how I perceived the 3D
image.
Something similar for the geometric 3D image when
parallel free viewing:
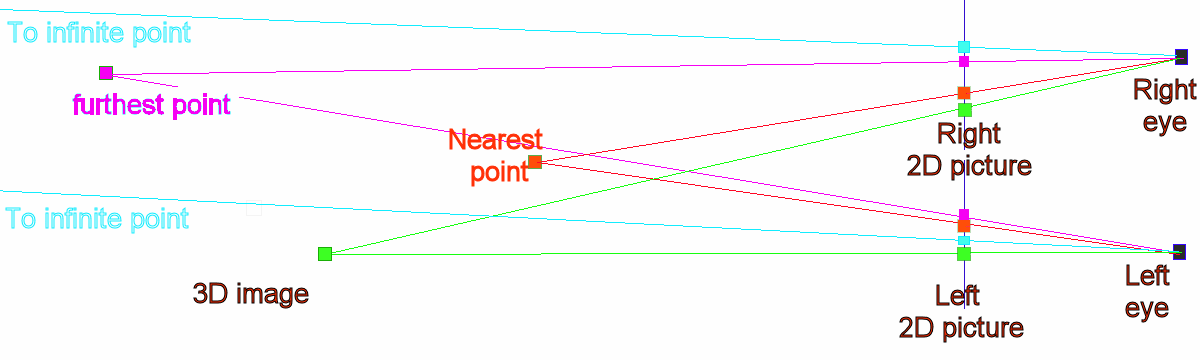 Parallel free viewing
Parallel free viewing
Some modeling of cross and parallel free viewing
As the 3D image is geometric, it is easy to do
calculations on:
3D image point
distance =
EyeSeparation*ViewDistance/(EyeSeparation-HomologousPointSeparation)
Vergence angle of
one eye =
atan((EyeSeparation-HomologousPointSeparation)/ViewDistance)
With:
HomolousPointSeparation is measured from the left point
to the right point (so negative for cross viewing)
Vergence angle: positive -> convergence angle and
negative -> divergence angle
Type 2: Picture size 3D image
In this case one can see the 3D image close to the location
of the screen. I assume this is due to size constancy (and
perhaps also the familiar size cue) of the size of the 2D
pictures.
This type might be a form of salient mode (see Rock, [
1995], page 44 and 45).
After having three months experience with cross free
viewing, this became the way how I perceive a 3D image.
Type 3: Immersion 3D image
One can perceive the 3D image as a fully immersed 3D image.
I assume this is due to size constancy (and perhaps also the
familiar size cue) of the actual object size in the 2D
pictures.
This type might be a form of salient mode (see Rock, [
1995], page 44 and 45).
I personally don't see a 3D image in this way (yet?). But
other people do (pers. comm. Berlin, L. [2009]).
Subtype 3a: Ortho 3D image
An immersion 3D image can also produce an ortho stereo 3D
image. When ortho stereo; the
Immersion,
Geometric 3D image
and 3D scene are the same.
Conclusion
The above all is just a draft and things are just forming in
the head;-).
The statement of Rock ([
1995],
page 45) on salient and proximal modes is important:
If this description of dual modes (salient
and proximal) of
perception is correct, it is no wonder that experiments
can lead to varying or contradictory results. Subjects
are caught in a potential conflict. If they match on the
basis of constancy, they fail to take note of one facet
of perception (visual angle); if they match on the basis
of visual angle (which is very difficult to do), they
fail to take account of the most central facet, namely,
constancy. Such an explanation sheds a different light
on the evidence of individual differences in constancy
experiments and the development of constancy.
The above matches almost the confusion we see when talking
about the stereo experience of people
Acknowledgments
I would like to thank the following people for their
help and constructive feedback: Larry Berlin,
Chris Evans, Bill Glickman, Jorn Lang
, Scott Steinman
and all other unmentioned people. Any remaining errors in
methodology or results are my responsibility of course!!!
If you want to provide constructive feedback, let me know.
Major content
related changes: Jan. 30, 2010