First and Last Crescent window prediction using Schaefer's
criterion
Introduction
The calculation of first crescent (FC) of the Moon depends on the
Moon's magnitude formula. A combination of Allen and Samaha's
formula (see this page) has been
used.
On other web pages, several comparison with Stern and
Fatoohi's papers, Kraus&Reijs (2012, page 22-23) and Reijs
(2011, #Confining) were made.
On this webpage some more attention will be given to the dependency
of the First Crescent window on the Latitude, AEC (Astronomical Extinction Coefficient) and Visual Acuity.
Also the Danjon limit (for most
Latitudes this happens at DAzi=0 and lowest AEC) will be looked at.
Also a check of the Last
Crescent (LC) window is done.
The visibility of FCs/LCs is a kind of window (aka FC window) for
altitude (Alt) and relative azimuth (DAzi) values.
Investigations has been done by looking a possibly better
formulas (based on Allen and the behaviour of inner planets'
[Mercury] phase curves or cube of phase angle). These
formula are though not based on empirical data; as such a
formula has not been derived yet (in 2022).
These results (based on Schaefer's criterion implemented in ARCHAEOCOSMO
package and sweph) will be compared to results from other criterions.
First Crescent window dependency on
Latitude
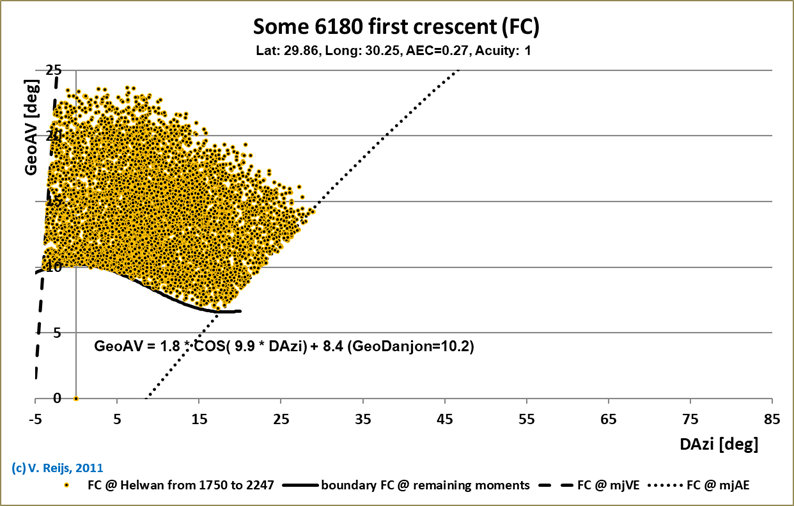
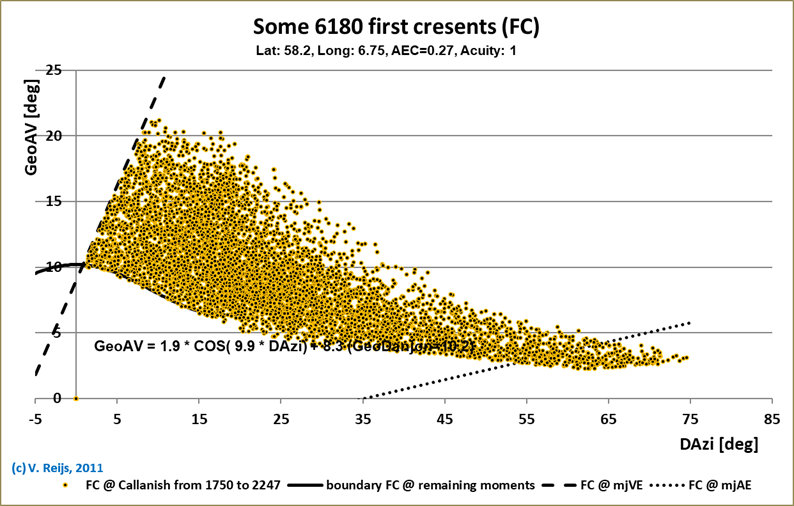
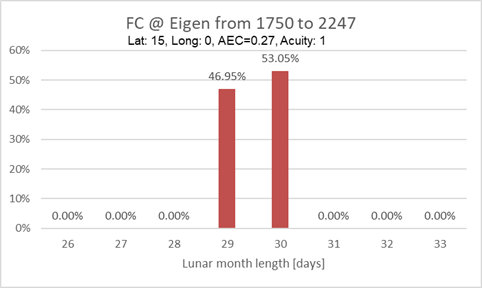
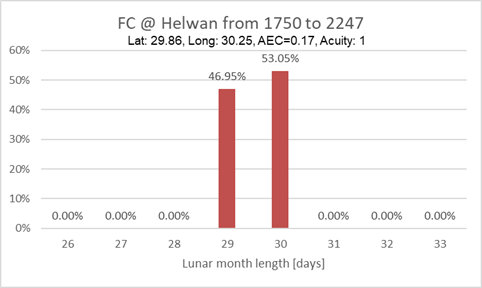
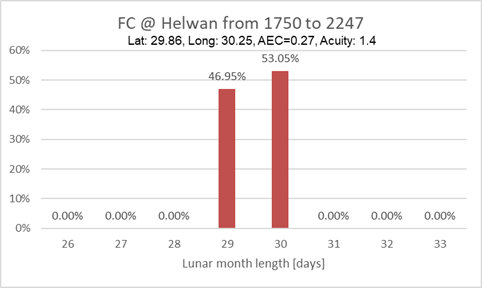
The First Crescent and Lunar month length over a 500 year period
is determined for Helwan (Lat=29.86°, Long=30.25°), Callanish I
(Lat=58.2°, Long=6.75°) and a Eigen location (Lat=15°,
Long=10°):
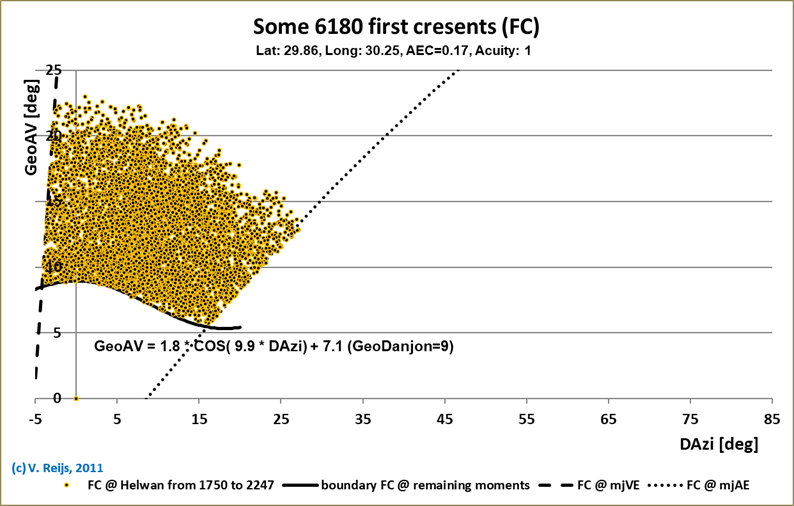
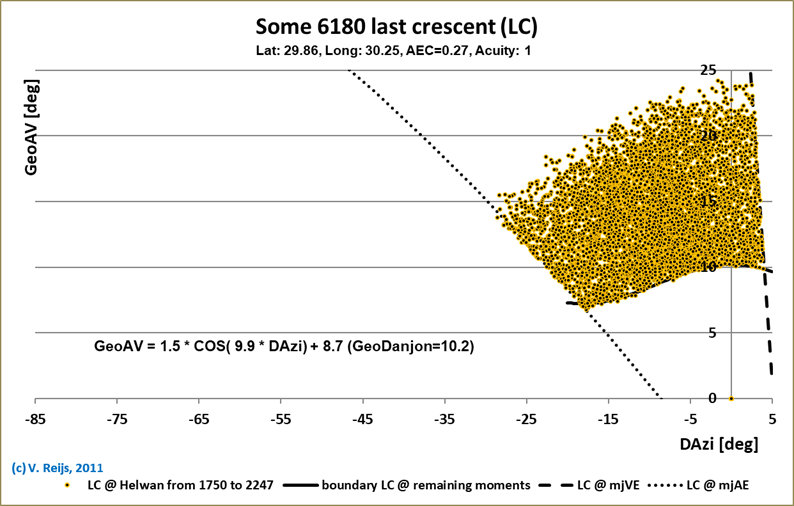
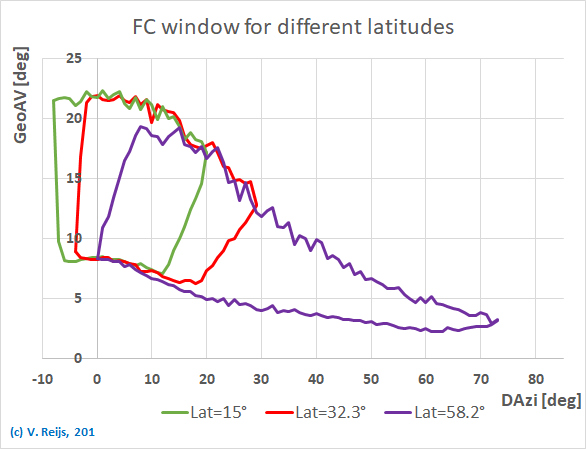
The form of the FC window for different GeoAV-DAzi combinations
changes in several ways when the Latitude is changed:
- The FC window looks to be most 'complete' (due to larger
variation of the Moon's position relative to the Sun's) for the
larger latitude (Callanish I), the FC window for Helwan and Eigen
location is cut by the line of FC Autumnal equinox
standstill.
- The limiting FCs on the right and left side (respectively the
dashed and dotted lines) are determined by the FCs around Vernal
and Autumnal equinox standstill events (Reijs, 2021, page 168
and Reijs,
2011, #confining).
- The Geocentric Danjon (GeoDanjon) limit (GeoAV @ DAzi=0°) is
for all shown latitude the same (around 10.2°).
<Remark: The TopoDanjon is around 1°
[parallax] smaller than GeoDanjon>
- Limiting FCs at the top and bottom have a similar-ish Alt
range at common DAzi.
The bumpy lines happen because only so many FCs happened at
these boundaries during 500 years.
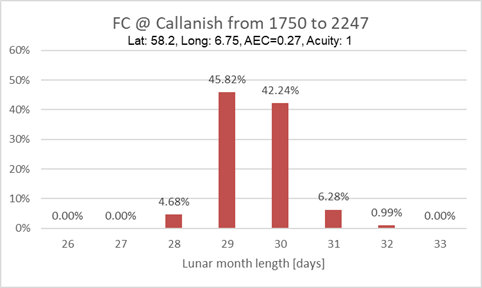
- The time between FCs (Lunar month) is restricted to 29 and 30
Days for Helwan and Eigen location, while for Callanish
I it varies between 28 and 32 Days (due to larger
variation of the Moon's position relative to the Sun's). The
durations shorter than 29 days or longer than 30 Days happen
when the FC is near equinoxial major standstill events.
So the time between FCs (Lunar month) at higher latitudes has a
larger range. Most literature [e.g. Samuel, 1972, page 14]
will only talk about 29 and 30 Days, which is quite true for
Egypt or Babylon (latitude lower than 32deg).
- For all shown locations the average lunation period is 29.531
Days (aka the Synodic
Month).
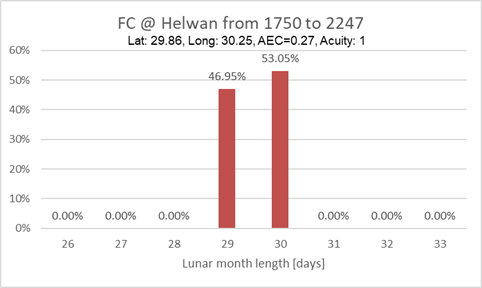
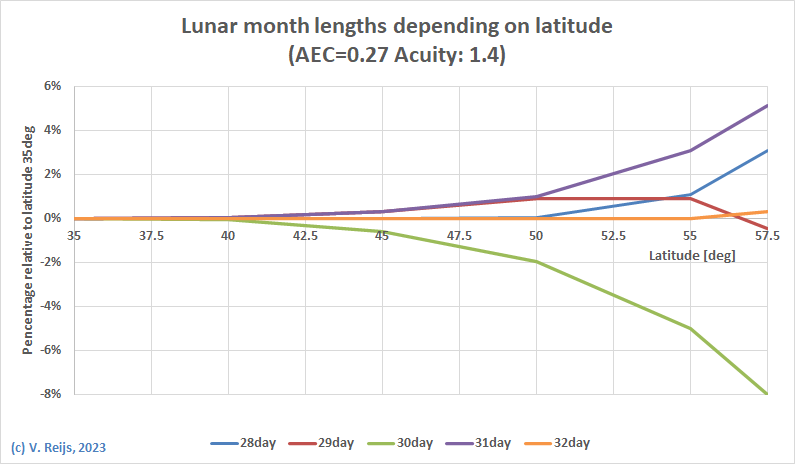
Length of the Lunar month
depending on latitude
Here is an graph where the Lunar month lengths (see also Schaefer, 1992) are
depending on the latitude
The percentages are referenced to a location (|latitude|<=
~35degrees) where only 29 and 30day Lunar month lengths happen. At
such a location 29days happen in 46.9% and 30days in 53.1% of the
cases, all other Lunar month lengths never happen: 0%.
This with AEC=0.27 and acuity=1.4
This with AEC=0.17 and acuity=1.4
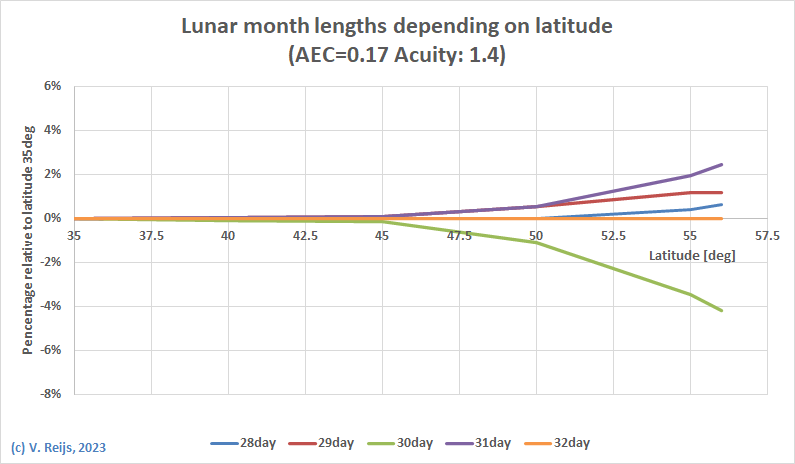
So above latitudes of 40deg, there will be Lunar months of 31days.
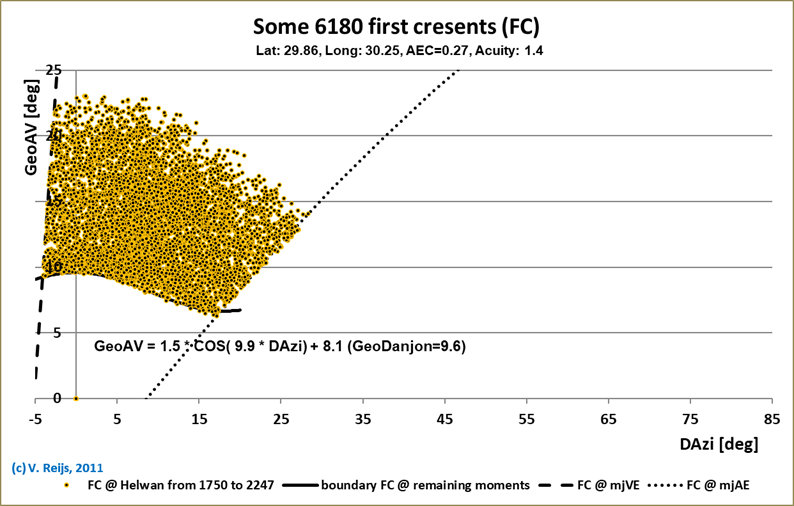
First Crescent window dependency on AEC
The GeoDanjon limit (GeoAV @ DAzi=0°) decreases with some 1.2° when
the AEC decreases from 0.27 to 0.17.
First Crescent window dependency on
Visual Acuity
The GeoDanjon limit (GeoAV @ DAzi=0°) decreases with some 0.6° when
the Visual Acuity increases from 1 (standard) to 1.4 (average).
Last Crescent window
The LC window (on the right) is similar, but mirrored along DAzi=0,
as the FC window (on the left).
Changing the Moon's magnitude formula
from Allen's to Allen+plus formula
Different formula of the Moon's magnitude (using Allen's,
Allen&Mercury's and Allen&Samaha's phase curve) are derived
on this
page. The resulting distribution of FCs can be seen below:
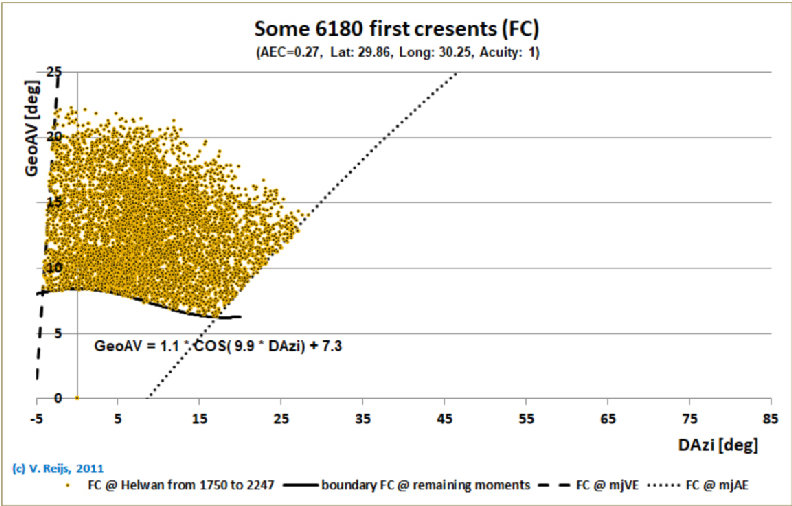
Using Allen's magnitude formula
(and [standard] Visual Acuity =1)
|
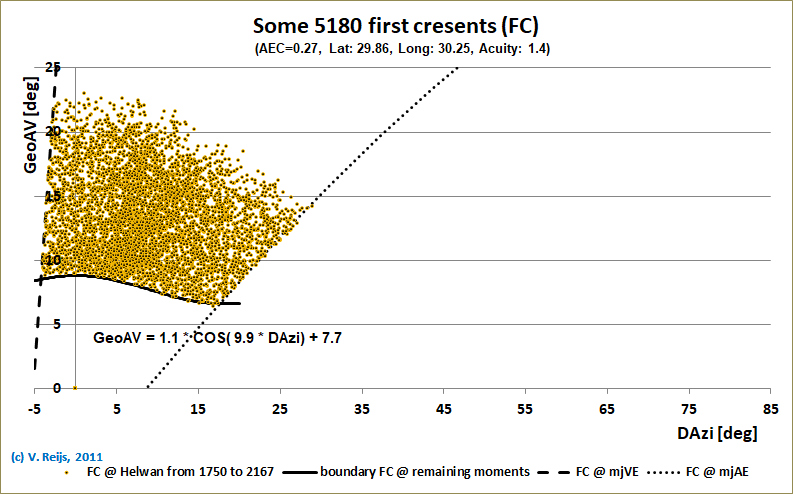
|
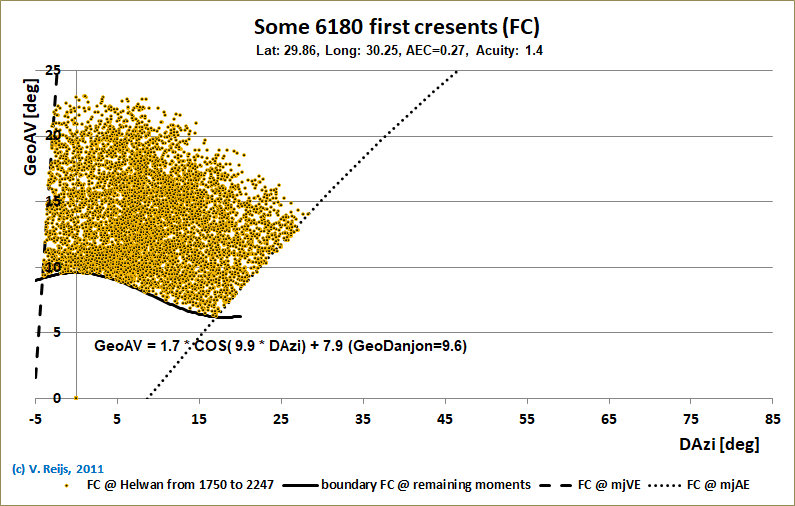
Using Allen&Samaha's
magnitude formula
(and [average] Visual Acuity =1.4) |
Crescent width and length
The phase angle for FC moments varies between 150 and 172deg:
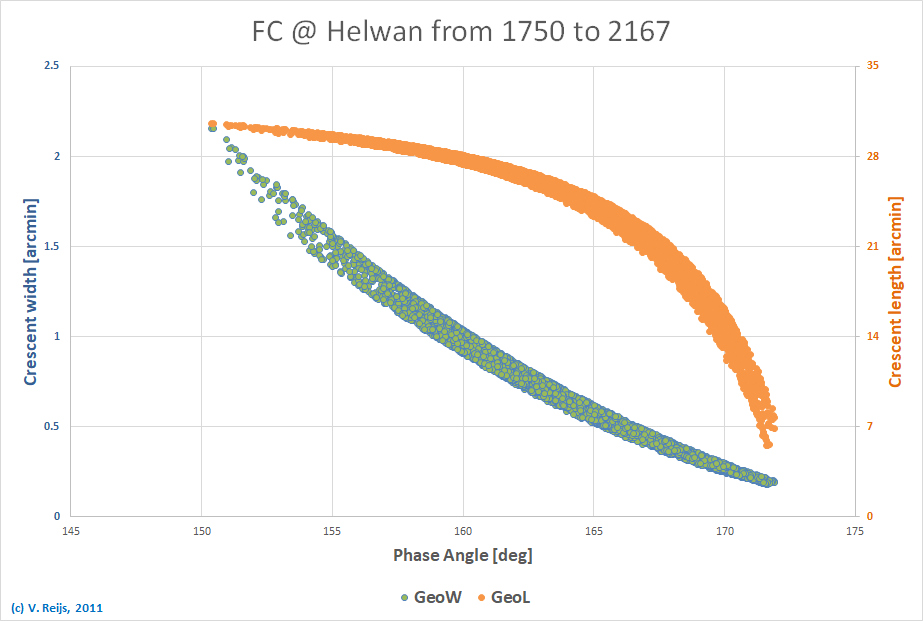
The crescent width varies between 0.2 and 2.2arcmin, while its
length is between 6 and 31arcmin (using Sultan 2005).
The object's apparent angular size below which an object is seen as
a point source (the CVA: Critical Visual Angle) is described by
Clark (1990, Figure 2.6). FCs
and LCs are normally seen between 0 and 30 minutes after Sun set,
and in that case the background brightness is some 13 Magn/arcsec2
(Clark, 1990, Table 2.3). This means that the maximum point source's
apparent angular size for these background brightnesses have a CVA
of around 1 arc-min. This is close (although slightly lower) to
crescent width during FCs (between 0.2 and 2.2arcmin).
Schaefer (Schaefer, 1991, page 271) relates the visibility of the
crescent to Lamar's findings:
"For naked eye observations, the critical portions of the
crescent are always narrower than the resolution of the
eye [CVA]. In such a case, the detection threshold does not
depend on the surface brightness of the Moon, but on the total
brightness integrated across the crescent (Lamar et al.
1947)".
If indeed a) narrower is related to crescent width (which is
for most FC/LC events smaller than the CVA) and b) total
brightness integrated across the crescent is the Magnitude of
the Moon at LC/FC events; we can evaluate the FC and LC visibility
of the Moon by using point source detection formula of Hecht.
I am still not 100% sure if the above is correct, let me know.
Comparison of Schaefer's and Segura
González' TopoDanjon limits
The TopoDanjon is defined from the centre of the Moon. The
implementation of Schaefer (in Swiss Ephemeris and ARCHAEOCOSMO)
though calculates the TopoAltitude (at DAzi=0) as if the crescent is
at the centre of the Moon. So to (approximately) determine the
TopoDanjon limit one has to add something close to the radius of the
Moon (something between 10 and 15arcmin) to the calculated
TopoAltitude (this has been done in all below calculated TopoDanjon
limit grahs).
Segura González criterion did not include the distance
crescent-centre of the Moon (pers. comm., June, 2023). In below
graph this has been inlcuded. In his newer work (since June 2023) he
has in corporated this.
Comparing the TopoDanjon limit (TopoAV at DAzi=0°) of Schaefer's
criterion (Lat=29.86°, Visual Acuity=1 or 1.4, and using three
different Moon magnitude formula) and Segura González criterion
(based on Helwan model) gives the below picture:
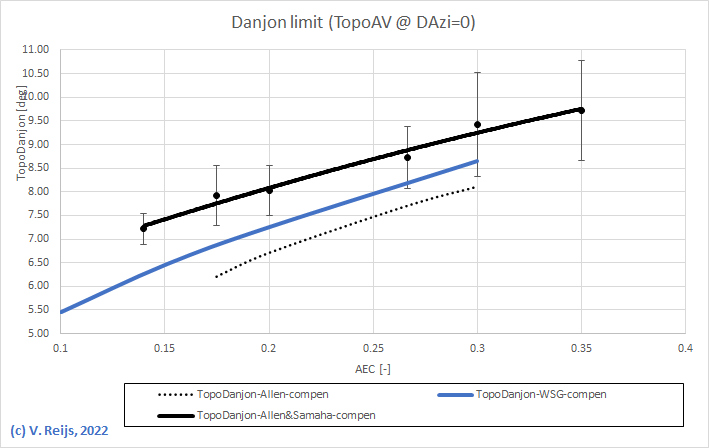
- TopoDanjon-Allen (black dotted curve, Visual Acuity=1)
Is derived with Allen's magnitude formula (using Swiss
Ephemeris, version 2.10.01 and ARCHAEOCOSMO). As Allen
calculates a too high Moon brightness for large phase angles,
the actual Topocentric Danjon limit curve should be higher. So
this TopoDanjon-Allen is not correct.
- The TopoDanjon-WSG (with compensation of Moon radius) of
Segura González (blue curve)
Is derived from his Topocentric phase angles (Segura González,
2021, Drawing 3). Segura González uses an adjusted
Moon magnitude formula, based on Russell's ideas that
resulted in lower magnitude for large phase angles.
By the way: the TopoDanjon is almost identical to
(180-Topocentric phase angle+radius of Moon).
- TopoDanjon-VR(Allen&Samaha) (black curve, Visual
Acuity=1.4)
Is using Samaha's cube of phase curve for the Moon magnitude
formula (using Swiss Ephemeris version 2.10.03 and
ARCHAEOCOSMO), as derived on this page,
*Remark: TopoDanjon-VR(Allen&xxx) could not
be determined below AEC=0.14, as the airmass formula could not
produce a lower value for the same geographical location of
Helwan (most specifically due to the height).
Error analysis
There are three errors that can be envisaged:
- the TopoDanjon has a standard deviation of 5 to 10% due to
standard deviation in AEC of around 20% [Schaefer 2000, page
128];
- the TopoDanjon has a standard deviation of around 0.25deg due
to standard deviation in Visual Acuity of around 0.2 [Ohlson, 2005]);
- the TopoDanjon limit has a standard deviation of around
0.03deg due to precision of graphically determining TopoDanjon
This reults in (1σ) error bars in the below TopoDanjon limit graph:

Danjon limit of other authors
In Table 1 of Segura González [2021] an overview of reported
Danjon limits is provided. His table has been reproduced and
included below:
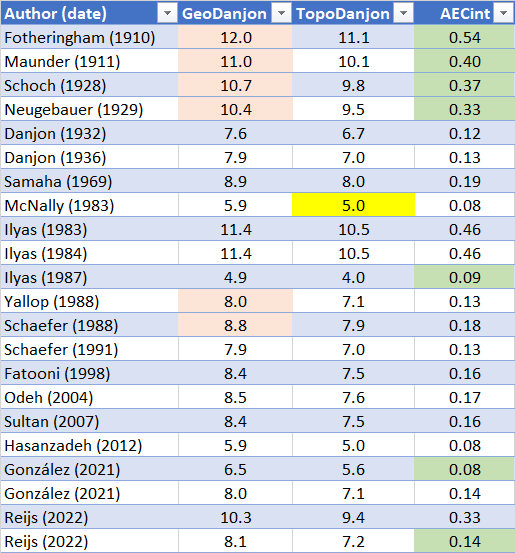
Cells with yellow background were assumed (by VR) to be reported
as TopoDanjon??? If not correct, let me know.
Cells with green background are documented for having a (very)
clear skies.
Cells with orange background were originally reported as
GeoDanjon.
The reported TopoDanjon (TopoAV at DAzi=0) values have been
related to an AECint (the last column) that is
calculated by using a fitted curve of
TopoDanjon-VR(Allen&Samaha):
AECint = 0.0092*TopoDanjon2 -
0.0658*TopoDanjon + 0.155
<remember this AECint is just an
indication, as the behaviour between AECint
and TopoDanjon is not really known>
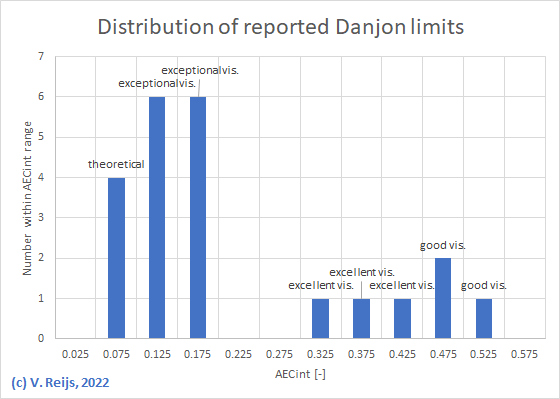
Most reports seem to related to an AECint
around 0.175 (based on TopoDanjon-VR(Allen&Samaha)): exceptional
visibility.
Some are very close or even lower than the theoretical minimum AEC
of ~0.12 (Rayleigh scattering).
It is interesting to see that all early reports (before 1930) have
a calculated AECint of 0.3 to 0.55
(excellent/good visibility), while the reports (according to
Segura González [2021]) talk about 'very pure skies'. It could be
that these authors use the same methodology for determining the AV
curve: calculating the average AV-angle at a certain DAzi, while
in more recent times it means the minimum AV-angle
(Kraus&Reijs, 2012, page 1, 23).
Conclusion
In some way it is amazing that the influence of AEC and Visual
Acuity is not really mentioned in the evaluation of the Danjon limit
such as in the article of Fatoohi (1998).
The new
Moon magnitude formula (TopoDanjon-VR(Allen&Samaha))
removes the known issue of Allen's magnitude (which was too high for
large phase angles).
When comparing the results of this new formula with for instance
Segura González' TopoAV, there is a difference of around 0.75degrees
Both TopoDanjon-WSG (black dotted curve) and
TopoDanjon-VR(Allen&Samaha) (black short-dashed curve) use
as a basis Russell's theoretical cube of elongation for large phase
angles.
The resulting TopoDanjon-VR(Allen&Samaha) is perhaps on the high
end of the exceptional visibility AECint values of other
authors. But is it is still reasonable.
It would be great if someone was able to measure the Moon's
magnitude for large phase angles, so we can replace the more
theoretical/analogical formula with an empirical derived formula. If
you know such an empirical formula, let me know.
Acknowledgements
I would like to thank people, such as Wenceslao Segura
González and others for
their help, encouragement and/or constructive feedback. Any
remaining errors in methodology or results are my responsibility
of course!!! If you want to provide constructive feedback, let me know.
References
Allen, C.W.: Astrophysical quantities. London, The Athlone press
1973.
Clark, Roger N.: Visual Astronomy of the Deep Sky. Cambridge
[etc.] : Cambridge University Press 1990.
Fatoohi, Louay J. et al.: The Danjon limit of first visibility of
the lunar crescent. In: Observatory 118 (1998), issue 1143,
pp. 65-73.
Krauss, Rolf and Victor Reijs: Babylonian crescent observation and
Ptolemaic-Roman lunar dates. PalArch’s Journal of Archaeology of
Egypt/Egyptology 9, https://www.academia.edu/2334725/BABYLONIAN_CRESCENT_OBSERVATION_AND_PTOLEMAIC_ROMAN_LUNAR_DATES
, 2012.
Ohlsson, Josefin and Gerardo Villarreal: Normal visual acuity in
17-18 year olds. In: Acta ophthalmoligica Scandinavica
83 (2005), issue 4, pp. 487-491.
Reijs, Victor M.M.: Benchmarking of Schaefer criterion. In:
http://www.archaeocosmology.org/eng/benchmarking.htm (2011),
Accessed Feb 6, 2021.
Reijs, Victor M. M.: How visible are celestial
objects? In. Gudrun Wolfschmidt and Susanne M. Hoffmann
(ed): Applied and Computational Historical Astronomy: Proceedings
of the Splinter Meeting in the Astronomische Gesellschaft, Sept.
25, 2020. Hamburg: tredition 2021. pp. 152-175.
Samuel, Alen E.: Greek and Roman chronology: Calendars and years
in classical antiquity. Beck 1972.Schaefer, Brad: Length of the
lunar crescent. In: Quart. J. Roy. Astronomical. Soc. 32
(1991), pp. 265-277.
Segura González, Wenceslao: Danjon limit: Helwan method. pp.
1-117 https://www.researchgate.net/publication/348622116_Danjon_Limit_Helwan_Method,
2021.
Segura González, Wenceslao: Magnitude
of the Moon at large phase angles. In: (2022).
Schaefer, Brad E.: The length of the Lunar month. In:
Archaeoastronomy, No. 17, (1992), pp. S32-S42.
Schaefer, Brad E.: New methods and techniques for
historical astronomy and archaeoastronomy. In: Archaeoastronomy:
The journal of astronomy in culture XV (2000), pp. 121-135.
Sultan, Abdul Haq: Explaining and calculating the length of the
new crescent Moon. In: The observatory 125 (2005), issue 1187, pp.
227-231.
Major content related
changes: November 10th, 2011 and 2022