Home
Up
Search
Mail
NEW
Accuracy of declination due to errors in latitude, azimuth
and altitude
The accuracy of the (apparent) altitude is very important
and sometimes even more important than accuracy of the azimuth! It
provides the greatest variation in calculating the declination a
celestial body. This can be seen for the following
evaluation:
sin(dec) = sin(lat)*sin(alt) + cos(lat)*cos(alt)*cos(azi)
With:
dec: geocentric declination of the celestial body that could be seen
along line
lat: latitude of the building
alt: altitude of the alignment
azi: azimuth of the alignment
The errors in declination due to the errors in latitude, altitude
and azimuth are (are verified by using Monte Carlos analysis):
declat=lat / cos(dec) * (cos(lat)*sin(alt) - sin(lat)*cos(alt)*cos(azi))
decalt=alt / cos(dec) * (sin(lat)*cos(alt) - cos(lat)*sin(alt)*cos(azi))
decazi=azi / cos(dec) * (- cos(lat)*cos(alt)*sin(azi)) (assuming alt is independent of azi)
dectotal= sqrt( declat^2 + 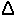decalt^2 + 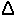decazi^2)
In this picture the behavior can be seen due to variations/errors in
latitude (.05o), altitude (.05o) and azimuth
(.05o) (with a mean latitude of 53o, a mean
altitude of 1o and an azimuth varying from 0o
to 360o). The effect of the altitude
error (yellow) is twice as much as the effect of the azimuth error (light
blue).
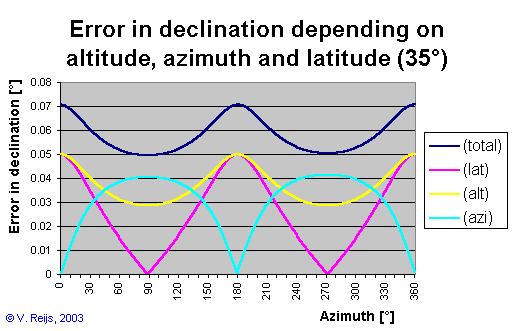
In the below picture the same conditions as above, except now at
mean latitude of 35°. Now the influence of error in altitude and
azimuth are sometimes comparable.
Disclaimer and Copyright
HomeUpSearchMail
Major content related changes: July 27, 2000