 Home
Home Up
Up Search
Search Mail
Mail
NEW
Evaluating the lunar observations on April 28th 2024
at Calanais I
Introduction
On tis web page, the ground proofing of the 3D scenery of
Calanais I site
within Stellarium is progressed from the ground proofing on March 31st
2024. On March 31st 2024 the azimuth difference was found to
be 0 +/- 0.01deg, which is equivalent to around 0 +/- 3sec.
A few levels might need to be reiterated:
- Determining the azimuth (rotation of vertical axis) of the 3D
laser scan
- Determining the tilt (rotation of East-West axis) 3D laser
scan to give the apparent altitude
- Determining if the whole 3D laser scan has to be vertically
and East-West transformed with respect to Cnoc and Turso's DSM.
These three levels are hopefully enough to get a good South
viewing skyline (from the end of the avenue: near stone 8 and 19).
More rotations/transformations could be needed, but that cannot be
determined with the present camera location.
Steps to ground proof the
Calanais I
3D scenery
On April 28th 2024 some 9 relevant photos were taken (by E. Rennie)
to record the Moon going over/through the Calanais I site. These photos
are being used to ground proof the Calanais I 3D scenery in Stellarium for the three mentioned
levels.
The following steps have been used for the preparation
- Camera
- FUJIFILM; Digital Camera X-T3
- The EXIF data (Create Date and Shutter Speed)
of the photos has been used to calculated: a photo's NTPtime
(= [EXIF Create Date] + Offset).
- Photo were taken with
this workflow
- Place camera on tripod as near as possible near stone 8 and
facing towards the circle, facing the circle (line E). The lens
is, in this physical world, at a height of 113cm measured from
the local ground. Zoom, so that some 10 stones are visible in
the photo. Keep zoom and position of camera during the whole
session the same. You migth need to rotate the camera.
- Timing
- For each photo, with its NTPtime, of the touch
moment is compared with the time in Stellarium when the Moon
also is at the touch moment: Moon in Stellarium.
- Tools
- The 3D scenery of Calanais I (version: callanish1_Readjusted20230821)
and added convergence_angle in the ini-file of:
-3.83588°) in Stellarium
(version 23.2) has been used.
- PSP (Coral Paint Shop Pro X9) was used to layer Stellarium
screen grabs on the photos
Photos taken on April 28th, 2024
Here is an overview of the photos used in this evaluation:
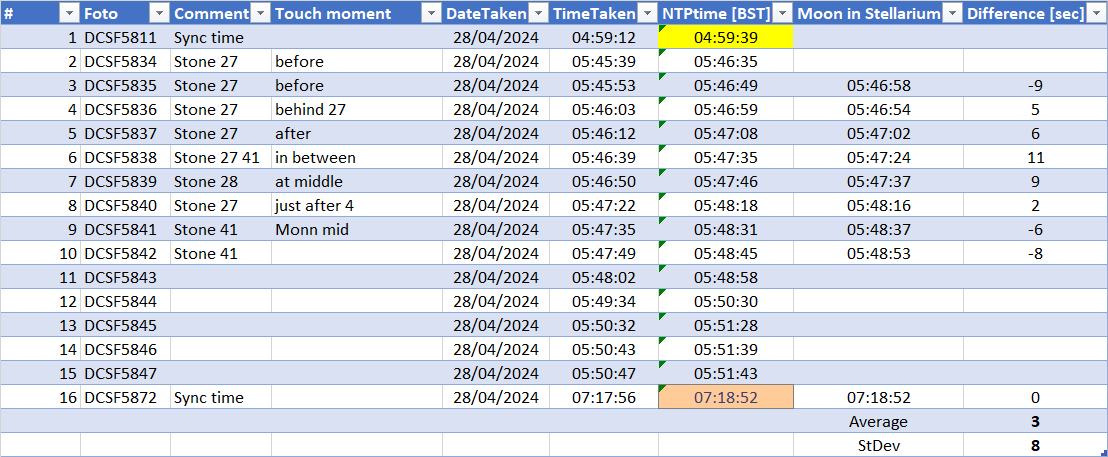
The first Sync. timed photo (DCSF5811) did not look to provided
consistent timings of the other photos. The last Sync. timed photo
(DCSF5872) though provided reasonable small differences.
So the timing difference in timing is: 3 +/- 8sec. The standard
deviation is larger than we found on March 31st, this is
due to the lack of real touch moments.
As the standard deviation is large compared to the photos taken on
March 31st, so we will not use these photos to make
another iteration in the ground proofing.
Next iteration
The results of 8th iteration (V13) was that the timing
difference is 0 +/- 4sec, or 0 +/- 0.8arcmin. One more
iterations (V14) was done, to do a conversion from Convergence angle
to RotVert . V14 still has
a small error (0.004deg=0.3arcmin), but too small to make a new
version.
|
Iterations from initial 3D scenery
|
1st*
|
2nd
|
3rd
|
4th
|
5th
|
6th
|
7th
|
8th
|
9th
|
230505
|
230817 |
230818 |
230818-2 |
230818-3 |
230818-4 |
230821
|
V13
|
V14
|
Start
|
RotVert
[deg] |
0
|
-0.184
|
-0.184 |
-0.184 |
-0.184 |
-0.184 |
-0.184 |
0.013
|
-0.055
|
RotEW
[deg] |
0
|
-0.118
|
-0.088
|
-0.088 |
-0.088 |
-0.088 |
-0.088 |
-0.088 |
-0.088 |
TransEW
[cm] |
0
|
0
|
0
|
0
|
-30 |
-30 |
-30 |
-30 |
-30
|
Transvert
[cm] |
0
|
-44
|
-44 |
-20
|
-20 |
-7
|
-7 |
-7 |
-7
|
TransNS
[cm] |
0
|
0
|
0
|
0
|
0 |
+18
|
0
|
0
|
0
|
| Proposed |
RotVert
[deg] |
-0.184
|
+0
|
+0
|
+0
|
+0 |
+0 |
+0.197
|
-0.068
|
-0.004
|
RotEW
[deg] |
-0.118
|
+0.03
|
+0
|
+0
|
+0 |
+0 |
+0 |
+0 |
+0
|
TransEW
[cm] |
+0
|
+0
|
+0
|
-30
|
+0
|
+0 |
+0 |
+0 |
+0
|
Transvert
[cm] |
-44
|
+0
|
+24
|
+0
|
+13
|
+0 |
+0 |
+0 |
+0
|
TransNS
[cm] |
+0
|
+0 |
+0 |
+0 |
+18
|
-18
|
+0 |
+0 |
+0
|
The initial 3D scenery is callanish1_Readjusted_20230505.
Experiences
Overall accuracy
We have been able to position the 3D laser scan properly within
the 3D scenery and the Moon's path. The accuracy is around
1arcmin, which is close to the accuracy of the 3D laser scan
(0.5arcmin). No major improvement in precision looks to be
possible.
Sequencing of adjustments
The best sequence of adjustments, by reducing interdependencies,
of rotations and transforms is:
- 3D laser scan RotVert
- 3D laser scan RotEW
- Cnoc an Turso DSM TransEW
- Cnoc an Turso DSM Transvert
Determining remaining rotation and transform
Of course there are still a transform (Cnoc an Turso's DSM in
North-South direction:
TransNS) and
rotation (3D laser scan around North-South axis:
RotNS)
possible; these are not yet investigated as these can't really be
determined using the camera location at stone 8. One would need a
camera location at stone 33 or 23 (and times of resp. set or rise
events of a celestial object).
A realistic
TransNS can't really be
determined (as the effect of this is marignal on celestial
directions).
The rotation
RotNS will not have effect on the
Cnoc an Turso's DSM, more on the positioning of 3D laser scan with
the celestial object.
Artefacts in the 3D laser scan
A few stones in the 3D laser scan have some triangulation
artefacts (these were found as they were handy for aligning the
celestial object: red areas); stone 32 (error some 2arcmin: due to
possibly wrong normal of some triangles); stone 26 (error some 2
to 3arcmin: missing left side top and small bit on the right side
top); stone 27 (error some 2 to 3arcmin: missing left side top);
and stone 28 (has a mushroomed top).
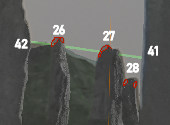
These errors make up a part the accuracy of the whole 3D scenery
(expected to be around 1 arcmin), so they are not that serious
except if these missing stone contours are used for defining
'touch' moments. It would have been nice on this observation day
to know the contours, as with a low Moon this precision would have
been handy.
It looks that Stone 49 is smaller (some 4 arcmin) in the 3D laser
scan than in reality (using a photo).
Acknowledgments
I would like to thank the following people for their help and
constructive feedback: Emma Rennie, Georg Zoti and all other
unmentioned people. Any remaining errors in methodology or results
are my responsibility of course!!! If you want to provide
constructive feedback, let me know.
Disclaimer and Copyright
 Home
Home Up
Up Search
Search Mail
Mail
Major content related changes: April 28, 2024

