HomeUpSearchMail
NEW

Babylonian lunar phenomenon

Lunar Three

• Lunation length of the previous month: 29 (hollow) or 30 (full) [days]
  In Babylonian text the lunation length of the previous month can be derived as they stated if the day of the first crescent being on the 30^th day (so previous month was 29 days: hallow month) or being on the 1^st (previous month was 30 days: full month).
• na (na in the middle of the month: first mentioned around 567 BCE) [uš]
  The time between sunrise and moonset on the day the moon sets for the first time after sunrise (in evening)
  
• KUR (first mentioned around 418 BCE) [uš]
  The time between sunrise and moonrise on the day the moon is seen for the last time (last crescent) (in morning)

Lunar Four

• na [uš]
  The time between sunrise and moonset on the day the moon sets for the first time after sunrise (in morning)
  
• ŠÚ [uš]
  The time between moonset and sunrise on the day the moon sets for the last time before sunrise (in morning)
  
• ME [uš]
  The time between moonrise and sunset on the day the moon rises for the last time before sunset (in evening)
  
• GE₆ [uš]
  The time between sunset and moonrise on the day the moon rises for the first time after sunset (in evening)

Lunar Six

• na_N [uš] (na of the 1^st day) [Lis Brack-Bernsen. "Goal-Year tablets: Lunar data and predictions." In Ancient Astronomy and Celestial Divination, edited by N.M. Swerdlow: MIT Press, 1999, page 168]
  The time between sunset and moonset on the day the moon is seen for the first time (first crescent) (in evening)
  
• na [uš]
  The time between sunrise and moonset on the day the moon sets for the first time after sunrise (in morning)
  
• ŠÚ [uš]
  The time between moonset and sunrise on the day the moon sets for the last time before sunrise (in morning)
  
• ME [uš]
  The time between moonrise and sunset on the day the moon rises for the last time before sunset (in evening)
  
• GE₆ [uš]
  The time between sunset and moonrise on the day the moon rises for the first time after sunset (in evening)
• KUR [uš]
  The time between sunrise and moonrise on the day the moon is seen for the last time (last crescent) (in morning)
  

Summations of Lunar Four values

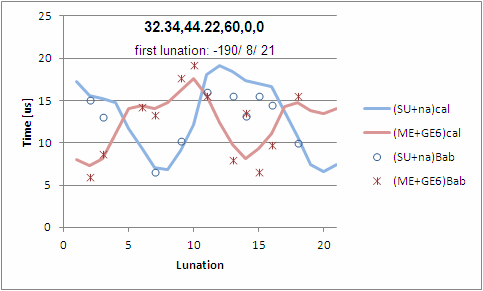
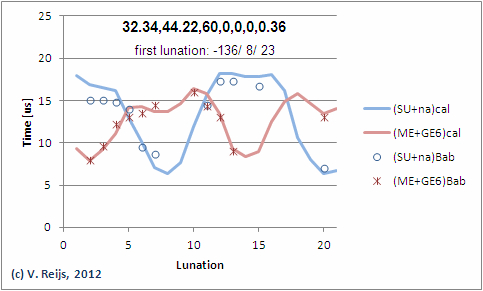
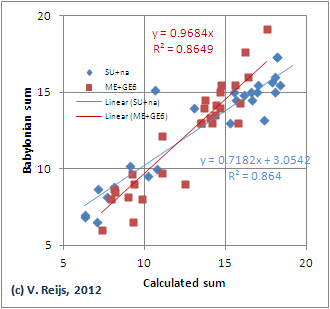
In interesting aspect of the Lunar Four is that if one make sums like: ŠÚ+na; ME+GE₆; and ŠÚ+na+ME+GE₆, these sums become almost independent of longitude, latitude and horizon altitude. This is ideal for determining a parameters independent of location. Below picture is calculated using ARCHAEOCOSMO: 

The spiky na curve (green) and smoother ŠÚ+na curve (blue)
<Remark: above na curve is slightly different then Brack-Bernsen's Figure 4 as that had a small ephemeris error [Pers. Comm. Brack-Bernsen, 2012]>

Brack-Bernsen showed e.g. that ŠÚ+na+ME+GE₆ is a very good way to determine the periodicy of Lunation-length P_Φ [Lis Brack-Bernsen, and Matthias Brack. "Analysing shell structure from Babylonian and modern times." In 10th Nuclear physics workshop, 1-13. Kazimierz Dolny Poland, 2003, page 10.]: ~411.8 days (being the HarmonicDifference(Lunar apse cycle, Tropical year)). (Meeus [2002], page 21-23)
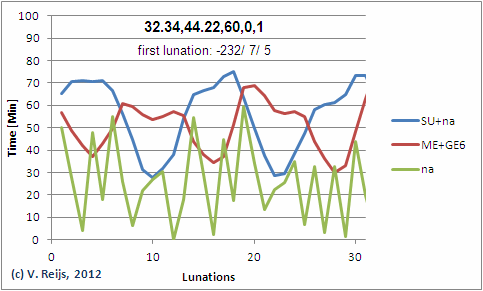
From ŠÚ+na and ME+GE₆ (above picture) one can relate the Tropical year with 12.368 Synodic months.

Predicting Lunar Six values: Goal-Year method

  Green curve is na_i while Blue curve is na_i-223 - 1/3*(ŠÚ+na)_i-223

Comparing Babylonian Lunar Four sums with DE406

A few Goal-Year Lunar Four values have been compared with values calculated with Swiss Ephemeris (using ARCHAEOCOSMO). The following method has been used:

• First a matching of the Babylonian lunation length with the calculated lunation length (using my implementation of Schaefer's criterion).
  
• When best match found; the ŠÚ+na and ME+GE₆ are calculated.
  
• With that info the below pictures are graphed
  

The form of the curves for the Babylonian and calculated values are comparable
<Remark: lunation 14 seems to be somewhat off, might be a scribe error?>
[LBAT 1251+1252, Hunger, 1999, page 91-94]


The form of the curves for the Babylonian and calculated values are comparable
[LBAT 1285, Hunger, 2006, page 269-275]

Difference between Babylonian measurements and calculated Lunar Four sum values

From the above graphs one can see there is a difference between the Lunar Four sum values of the Babylonians and the calculated ones:

The 1σ seen between Babylonian and calculated Lunar Four sums is around 1.5 [us]. As this is a sum of two Lunar Four values; the 1σ of each Lunar Four values is around 1 [us] (1.5/√2). This errors looks large compared to what is found during evaluation of eclipses (Stephenson and Fatoohi, 1994). They found that 1 hour is equivalent to 15.3 +/- 0.5 [us] (page 109) for dates after 300 BCE. This would a 1σ of around 0.1 [us] (0.5/√15). They also found no seasonal changes.
So this larger than expected error is unlikely to be explainable due to the impreciseness of the Babylonian water clocks around 200 BCE. Would there be a systematic measurement procedure difference?

Disclaimer and Copyright
HomeUpSearchMail