Mail
NEW

Modes due to lunar and solar periods

Some cycles with lunar and solar periods are known in astronomy and history:

Metonic cycle
Metonic cycle incl. sidereal months
Saros cycle

For these cycles it has been calculated when the lunar/solar month/year period fit best on a certain Date (unsing the FDM). Comparable studies can be done for other cycles (if you want a cycle to be covered, let me know).

I have kept the durations of all periods te same, although they slowly change over time: the durations of period , which I used in the below evaluation, changes only some 0.000007% over the 410 years.

Metonic cycle

The following method has been used for the Metonic cycle:

In steps of 0.1 day and from an arbitrary Date (Date=0), the quotient of Date and every month or year period has been calculated and thus one knows how much a certain month/year period differs from a precise fit (a whole number).
On Dates with (almost-)fits, the difference with multiples of the tropical year is determined. The tropical year is taken because on these Dates, the phase of the moon (synodic) will change slower than the sun's position (tropical).
If the absolute value of the tropical difference is smaller than 1 day, it has been plotted in a graph.

The following graph is obtained for the Metonic cycle; every symbol is a point where the difference (with regard to a precise fit) was smaller than 1 day:

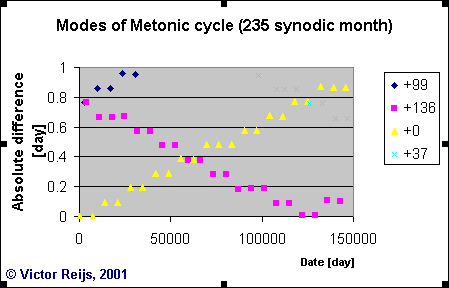What can be seen in the above graph:

Equal colored symbols in a graph shows a series of Dates that repeat themselves with the cycle-studied. I call a colored serie: a mode (somewhat analogue to modes in standing waves).
The only difference between the modes (colored series) is that they have a delayed Starting Date. So for instance the purple mode in the Metonic graph has it's first almost-fit not on Date=0 but on delayed Starting Date=136 synodic months.
The graph seems to repeat itself around Date=129000 days (look at the repeating form of the graph and the repeating relative Starting Dates). I assume there is a good reason for this (if you know of similar periods in literate, let me know). It looks to be 12*synodic month*tropical year.
The modes with the smallest solar difference are with Starting Date of 0 and then taken over by mode with delayed Starting Date of 136 synodic months

Metonic cycle incl. sidereal months

The following method has been used for the Metonic cycle incl. sidereal months:

In steps of 0.1 day and from an arbitrary Date (Date=0), the quotient of Date and every month or year period has been calculated and thus one knows how much a certain month/year period differs from a precise fit (a whole number).
On Dates with (almost-)fits, the difference with multiples of the sidereal month is determined. The sidereal month is taken because on these Dates, the phase of the moon (synodic) and sun's position (tropical) will change slower than the place of the moon with regard to the stars (sidereal).
If the absolute value of the sidereal difference is smaller than 1 day, it has been plotted in a graph.

The following graph is obtained for the Metonic cycle incl. sidereal months; every symbol is a point where the difference (with regard to a precise fit) was smaller than 1 day:

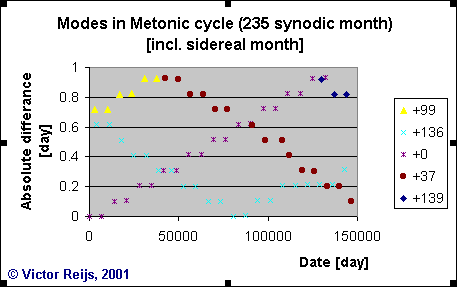What can be seen in the above graph:

Equal colored symbols in a graph shows a series of Dates that repeat themselves with the cycle-studied. I call a colored serie: a mode (somewhat analogue to modes in standing waves).
The only difference between the modes (colored series) is that they have a delayed Starting Date. So for instance the light blue mode in the Metonic graph has it's first almost-fit not on Date=0 but on delayed Starting Date=136 synodic months.
The graph seems to repeat itself around Date=80500 days (look at the repeating form of the graph and the repeating relative Starting Dates). I assume there is a good reason for this (iif you know of similar periods in literate, let me know).
The modes with the smallest lunar difference are with Starting Date of 0 and then taken over by mode with delayed Starting Date of 136 synodic months

Saros cycle

The following method has been used for the Saros cycle:

In steps of 0.1 day and from an arbitrary Date (Date=0), the quotient of Date and every month period has been calculated and thus one knows how much a certain month period differs from a precise fit (a whole number).
On Dates with (almost-)fits, the difference with multiples of the draconic month is determined. The draconic month is taken because on these Dates, the phase of the moon (synodic) and the closeness of the moon to the earth (anomalistic) will change slower than the lunar position near the ecliptic (draconic).
If the absolute value of the draconic difference is smaller than 1 day, it has been plotted in a graph.

The following graph is obtained for the Saros cycle; every symbol is a point where the difference (with regard to a precise fit) was smaller than 1 day:

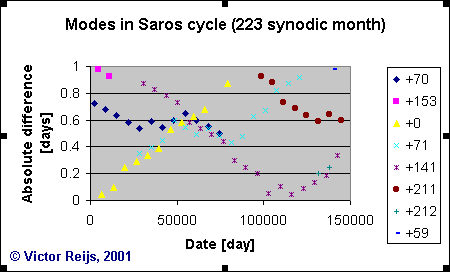
What can be seen in the above graph:

Equal colored symbols in a graph shows a series of Dates that repeat themselves with the cycle-studied. I call a colored serie: a mode (somewhat analogue to modes in standing waves).
The only difference between the modes (colored series) is that they have a delayed Starting Date. So for instance the dark purple mode in the Saros graph has it's first almost-fit not on Date=0 but on delayed Starting Date=141 synodic months.
The graph seems to repeat itself around Date=110000 days (look at the repeating form of the graph and the repeating relative Starting Dates). I assume there is a good reason for this (if you know of similar periods in literate, let me know). It looks to be 5*draconic month*synodic month*anomalistic month.
The modes with the smallest lunar difference are with Starting Date of 0 and then taken over by mode with delayed Starting Date of 141 synodic months

General remarks

The above graphs provides some insight what and how people in former times could have measured/experienced similar occurrences, if they would have historic tables/tallies of information. In my opinion, they should at least have this information for several occurrences, say 50-100 years, otherwise accuracy could be too low.

Disclaimer and Copyright

Home

Mail

Last major content related changes: May 5, 2001