HomeUpSearchMail
NEW

Megalithic measures by Thom

Megalithic Fathom

• No a priori knowledge of some periodicy in the diameter
• The offset (b) may be different from zero

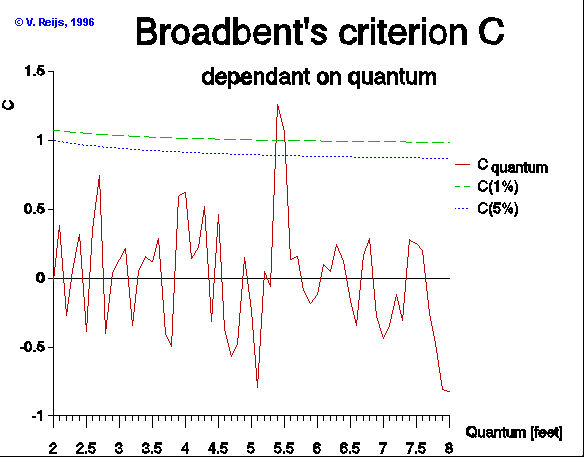
This picture tells us when a possible periodicy (quantum) provides statistical confidence (when C_quantum>=C(1%)~1). So using the table of measured diameters from the Thom book, this happens at 5.44 [feet]. Thom calls this length the Megalithic Fathom (1967, page 41).

Analyzing this deductions, I come to the following issues:

• Thom makes the b (the y-axis offset) equal to zero, but using category Case IIb, one sees a b of some 0.3 [feet], this is not zero compared to the so called Megalithic Fathom (which is 5.44 [feet])!
• Did Thom measure the radius or the diameter of the circles? It is very important to know, because depending on the method, the variation will be different. It is expected that he measured the diameter (see also text with table 5.1 of him).
• Thom deducts (page 41) from the fact that:
radius = diameter / 2
that
megalithic yard = Megalithic Fathom / 2
The question is, is one allowed to do this on statistical grounds!? I would say no, because diameters are measured by Thom and not radius. If he had measured the radius then perhaps the megalithic yard would have popped up.
Remember that determining the radius is not easy! One has to know where the center of the circle is and this introduces another error.
• One is perhaps allowed to divided by two, if it is for sure that neolithic man made a stone circle by using a string and a pin in the ground at the center. If the length of the string (the radius) was set out with the help of the megalithic yard, then the diameter would be set out by a Megalithic Fathom.
• I think Thom should not have divided the Megalithic Fathom by two (there is no valid reason for that!). The Megalithic Fathom should have been good enough. Other people (like Kendall, Freeman and Barnatt and Moir) have found a measure that is coparable to the MF.
• Hawinks G. (Beyond Stonehenge [1973], page 241) assumes that people linking hands wirst to wirst will average double the meglalithic yard of Thom. This is comparable to my ideas.
• A good natural standard is available for determining the Megalithic Fathom, see my explanation.

• Some calculations have been done using the data set of Thom (table 5.1). This data set has been used as the base to calculate the standard deviation (using Monte Carlo analysis) . The following is analyzed:
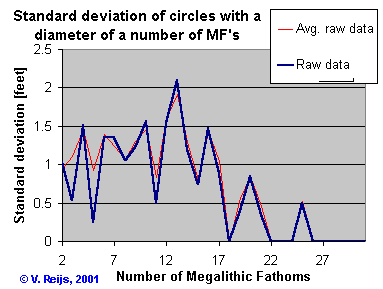
• The raw data set of Thom  is used. The standard deviation has been calculated for every group of circles that were build with an equal number of quantum's (blue). (C_5.44~ 1.3). Also a Monte Carlo analyses (the average is taken over 23 runs) is determined assuming an s of 0.33 foot (table 5.1) in the circle diameter (red). (C_5.44 ~  1.3)


 
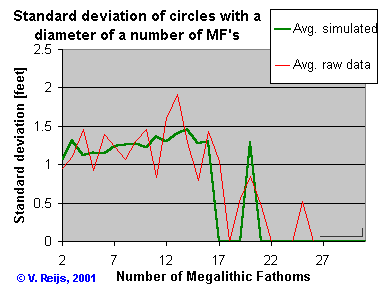
• The same distribution of number of quanta in the circle diameter as above. The quantum is now the human height (5.40, s=0.095 ft) and it includes an overall variation (b=0, s=1.15 ft). The behavior of the average standard deviation using Monte Carlo analysis (dark green) and the average standard deviation of the raw data (red) are almost same (the averages are taken over 23 runs). (C_5.40 ~  1.1)


• If using a standard rod (5.440, s=0.003 ft) with an overall variation (b=0, s=1.3 ft). The following standard deviation is gotten (light green): (C_5.44 ~  1.5)


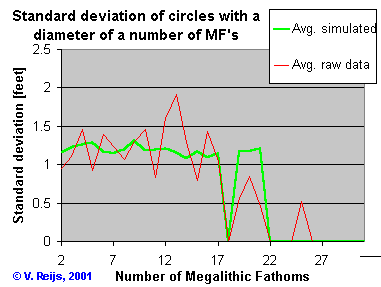
So comparable standard deviations and correct Broadbent values are delivered in both cases using a standard length. So a standard (like a standard rod: 5.440, s=0.003 ft or the human height: 5.40, s=0.095 ft) and a random uncertainty (e.g. due to width of standing stones: s=1.3 or 1.15 ft) gives comparable results as the measured circle diameters by Thom, and using the Megalithic Fathom (and not the megalithic yard).

• Is the Broadbent method still the best way to deal with periodicy (quantum's) in measurements? Or are there already better methods available?

Megalithic inch

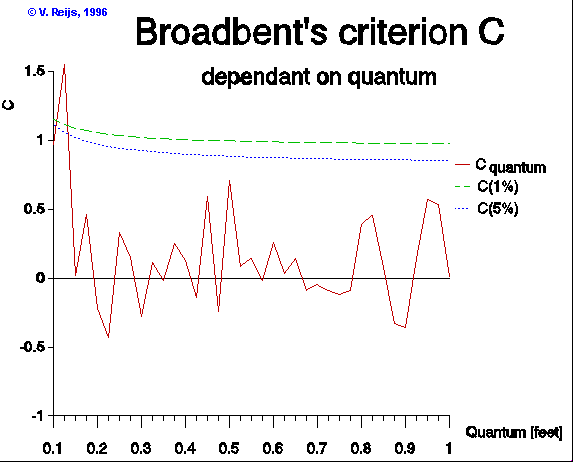
There is no real likeness of a quantum at 0.817, but another strange thing is that Thom now does not use the factor two that has been discussed in the above section!

A paper that discusses the megalithic inch (by Alan Davis, paper in Records in stone), finds beside 1 MI also quantum's of close to 3 MI and close to 5 MI (1% probability level).
He also provides an other idea, supported by me, why 3 MI, 5 MI, 1 MI, 1 MY, etc. could be common:
Alternatively, one might justifiable argue that the 5 MI quantum is very close to the mean width of a human hand, and interpret 1 MI as a mean finger width. It would be extremely difficult, if not impossible, to distinguish between these two hypothesis on the basis of present data.
I fully agree with this statement!

Related link

• http://discovery.syninfo.com/BEI/beiaaf.html

Disclaimer and Copyright
HomeUpSearchMail