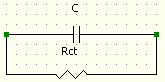HomeUpSearchMail
NEW

Lumped parameters (acoustic -> electrical)

JavaScript calculations can be done below.

The acoustical parameters of the elements can be translated to electrical parameters. I am using information from Calvert [2003], Kinsler ([2000], chapter 8.9 and 10.8) and Colman (pers. comm. [2006]). In the below it is assumed that the acoustic circuit is in size much smaller compared to the acoustical wavelength and that it is the air.

I am wondering how well the below theoretical model works for attenuation/resistance, reading this:
The attenuation of sound in air due to viscous, thermal and rotational loss mechanisms is simply proportional to f 2. However, losses due to vibrational relaxation of oxygen molecules are generally much greater than those due to the classical processes, and the attenuation of sound varies significantly with temperature, water-vapour content and frequency.
More study is needed to include at least molecules level attenuation and influence of humidity. I hope that within the environment of neolithic buildings these influence are not large (except the humidity perhaps). Help is needed!

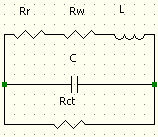
Acoustical inductance of a pipe

L' = ρL/(πa2) [H'] Kinsler [2000], formula (10.8.1) and (10.9.5)
 
with:
ρ = air density: 1.293 [kg/m3] (0°C, 1 atm)
L = effective length of pipe [m]
a = radius of pipe [m2]
L lumped

Acoustical resistance of a pipe

Thermal and viscous resistance due wall losses in pipe

Non capillary pipe

Rw' = (1.46*L/(πa3))√(4πρηf) [Ohm'] Kinsler [2000], formula (10.8.10) and (10.9.5)

with:
η = dynamic viscosity of air, 1.71 x 10-5 [kg/m-sec] (0°C, 1 atm)
f = frequency [Hz]

Capillary pipe (Reynolds number is less than 2000)

Rwc' = 1.46*8ηL/(πa4) [Ohm'] Oban [2003], factor 1.46: Kinsler [2000], formula (8.9.19)

Radiation resistance (open segment)

Rr' = 2πρf2/c (flanged) [Ohm'] Kinsler [2000], formula (10.8.9) and (10.9.5)
Rr' = πρf2/c (unflanged) [Ohm'] Kinsler [2000], formula (10.8.9) and (10.9.5)

Acoustical capacitance of rigid container/cavity

C' = V/(ρc2) [F'] Kinsler [2000], formula (10.8.4) and (10.9.5)

with:
c = sound speed in air: 331.5 [m/sec] (0°C, 1 atm)
V = volume of container [m3]
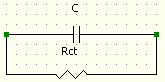
C lumped

Thermal resistance in container

Rct' = ρc2/(0.46*√(πηf/ρ)*A) [Ohm'] Coltman, pers. comm [2006]

with:
A = area of cylinder with radius a and length 2*a, where a is such that the cylinder has volume V

Helmholtz resonator

Helmholtz lumped

Frequency

fhelm = 1/(2π√(L'C')) [Hz] Calvert [2003]

Quality factor

Qhelm = 2πfhelmL'*( 1/(Rw'(fhelm)+ Rr'(fhelm))+1/Rct') [-]

Calculations

Browser must have JavaScript enabled
As example a Florence flask is used.

Temperature:       [ºC]
Air pressure:      [mbar]
Air humidity:      [%] (not implemented yet)
Radius of pipe:    [m]
Effective length:  [m]
Frequency:         [Hz]
Flanged:           (flange must be bigger then wavelength)
Volume container:  [m3]

Air density:       [kg/m3]
Air speed:         [m/sec]
Air viscosity:     [kg/m-sec]
L':                E [H']
Rw':               [Ohm']
Rwc':              [Ohm']
Rr':               [Ohm']
Rt':               [Ohm'] {max(Rw',Rwc')+Rr'}
C':                E [F']
Rct':              E [Ohm']
fhelm:              [Hz]
Qhelm:              [-]
Rthelm':            [Ohm'] {1/(1/(Rw(fhelm)'+Rr(fhelm)')+1/Rct(fhelm)')}
Disclaimer and Copyright
HomeUpSearchMail
Major content related changes: Jan. 20, 2006