HomeUpSearchMail
NEW

The length of the astronomical seasons

${\displaystyle declination={sin}^{-1}(sin\left(Obliquity\right)\cdot cos(\frac{360\cdot n}{Tropicalyear}+\frac{2\cdot Eccentricity\cdot 180}{\pi }\cdot sin\left(\frac{360\cdot (n-n_p)}{Anomalisticyear}\right))}$

With:
n: number of Days after summer solstice day
n_p: the position of perihelion seen from summer solstice in Days. I determined them using  SkyMap Pro 9 (these values are different then in Ruggles [1999, page 54]):

Tropicalyear: length of Tropical year
Anomalistyear: length of Anomalistic year
Obliquity [°]
Ecccentricity [-]

The below figure provides insight in the length of the astronomical seasons based on the above formula:

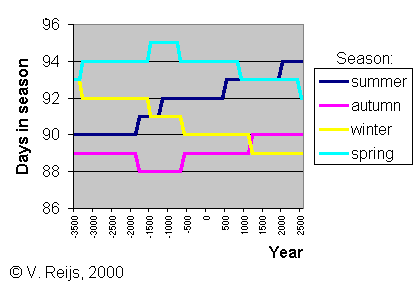
Following modern definitions of the astronomical seasons:

• Summer
From summer solstice (max. declination) until autumn equinox (declination=0)
• Autumn
From autumn equinox (declination=0) until winter solstice (min. declination)
• Winter
From winter solstice (min. declination) until spring equinox (declination=0)
• Spring
From spring equinox (declination=0) until summer solstice (max. declination)

Definition of equinox

1. the date when set and rise azimuths of sun (on one day) are opposite (180º) to each other. No counting of days is needed (is easy to determine). Will come close to modern definition of equinox, if horizon altitude is the same for set and rise positions.
   
2. the date that the sun's rise (or set) azimuth is half way the rise (or set) azimuths of winter and summer solstice (is quite easy to determine). If the rise (or set) altitudes are the same for solstices/equinoxes, this will provide an equinox date close to the modern definition (although it does not account for the variation due to Climatic precession changes).
   
3. the date that the sun is again at the same location after 182/183 days (is relatively easy to determine). Method used by Thom ([1967], page 109). This will have the 'equinox' declinations at around 0.5º
4. the date half way the summer and winter solstices dates. Remember half way the solstice dates is difficult to determine due to slow movement of sun around these solstices (thus not easy to determine).
5. the date when the sun rises due east or sets due west. In this case the concept of east/west must be known and to reach the modern equinox definition the horizon altitude must be 0º.
6. From DIO web-site:
   "Equinoxes are not (and were not anciently) determined “near sunrise and at sunset” as ... asserts, and that cannot be true for the equinox of 132 AD, which was allegedly observed at 2 PM. Ptolemy says his equinoxes were determined by noon observations using a ‘meridian” transit instrument (Almagest 3.1’s reference to I.12; Toomer p 61) which only can observe on the meridian."
7. the modern definition (declination = 0), will be quiet unlikely for neolithic man, because the concept of the ecliptic was not yet known (I think). But an indirect effect of declination is a straight line shadow of a top of a pole (see the horns of the solstices).
8. The date a gnonom casts a straight solar shadow on the plate.
   
9. The date that the Full Moon and Sun swap their rise (or set) place on the horizon (so when the Sun first rises e.g. more northern than the Moon). This concept is thought of by C. da Silva [2004], which in its turn is mentioned by F. Silva (Equinoctial full moon models and non-Gaussianity: Portuguese dolmens as a test case, [2011]) and calls it 'Megalithic Equinox'. This is around a declination of plus or minus 4 degrees.
   

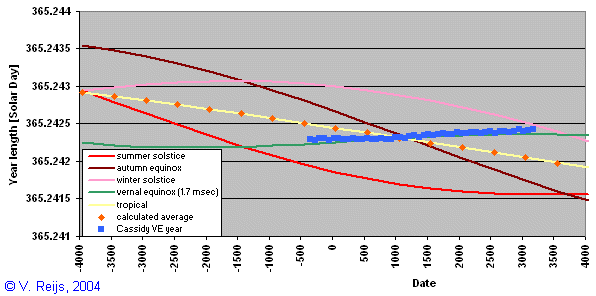
Vernal equinox year

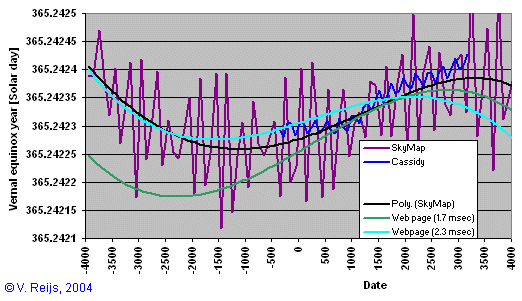
The calculated (green) values (with a change of 1.7 msec per century for Solar day, Stephenson [1997, page 514]) are quite close to SkyMap Pro 9's values (around 2 sec for the period 2500 CE to 400 BCE). This graph is quite different from the SkyMap values when looking before 400 BCE.
Two things can be seen:

• If I take a change of 2.3 msec per century for Solar day, the above results (light blue curve) for former years gets closer to the SkyMap results.
  SkyMap Pro 10  (like Cassidy) uses Stephenson & Houlden [1986] for DeltaT and n-dot of -26 ["/cy²], which can explain the 2.3 msec per century. SkyMap Pro could be changed in future (pers. comm. C. Mariott [2004]).
  
• The above sinusoidal function (green values) seen in the vernal-equinox year seems to be somewhat out of phase and/or period. This needs more investigation.
• As Cassidy says; the vernal-equinox year (green line and blue squares) is quite stable over the present years (while the other event years change more) and that is why he thinks that vernal equinox could have been chosen as the start of the year.
  Looking at the below graph, winter-solstice (pink line) was also quite stable around neolithic times, so could this have been the start of the year in neolithic time...  So I doubt if Stonehenge was following the vernal-equinox start of the year as discussed by Cassidy.
  But to be honest, I don't know if neolithic man was able to determine this temporal stableness of the mean winter-solstice/vernal-equinox year without having accurate clocks.
  The vernal-equinox and winter-solstice years do not quite follow the average event years of course (=mean tropical year):
  
  
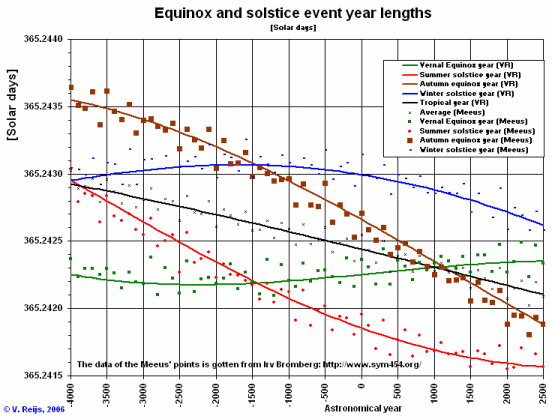
• The above formula has been checked with Meeus' formula, using information from Irv Bromberg [Pers.comms 2006]:
  
  
  
  
  There is not much difference (max. 17 sec [1 sigma]) between my formula and Meeus'. This difference is somewhat larger then the normal variation (5*60/100 = 3 sec) of a year.
  

Disclaimer and Copyright
HomeUpSearchMail