 Home
Home Up
Up Search
Search Mail
Mail
NEW
Planetarium programs
Introduction
In archaeoastronomy a possible accuracy of 0.5°
is expected for monuments build around 4000 BCE. On this web page I
try to determine the accuracy achievable with computer programs that
simulate the celestial events. The accuracy of these programs should
at least be around one order better than the presumed accuracy of
the monuments; so the accuracy must be much smaller than 30'.
This page will provide some insight on who to make a choice in
planetarium computer programs. This will be done along the
following lines:
The specification
A few features are important when looking at programs for
archaeoastronomical work. The following features should be taken
into account when deciding to use a program (in order of
preference):
- celestial objects
In any program (demo, share or free-ware) all planets, objects
and stars which are visible with the naked eyed need to be
available. Including an outline of the milky way and the horizon
- it should included all 'normal' theories of calculations
Such as: position (VSOP87, DE405, etc.),
aberration, perturbations, precession of
Equator (Capitaine N. [2005]), DT (Stephenson, etc.), nutation,
change of obliquity, lunar motion (n-dot,
ELP2000-85, etc.), proper motion (Hipparcos
and Tycho catalogues), light travel time, refraction, horizon dip, etc.
- has to have an accuracy of much smaller than 60' for azimuth
and altitude between 4000 BCE and 2100 CE. This specification
has to be relaxed perhaps for the moon.
- provide an inaccuracy range in every display, based on for
instance Monte Carlo Analysis
- the possibility to step in time using different periods;
like average solar periods (hours, days, sidereal day,
tropical year, etc.) and average lunar periods (like draconic,
synodic, nodal cycle, etc.).
- has to have an automatic date/time increase/decrease repeat.
- the possibility to define a sky
window and determine when a celestial object passes
along this window.
- information on and changing the actual DT used by the calculations.
- provide visibility (incl. e.g. extinction
angle) of celestial objects in the sky (depending on
twilight conditions).
- integrate it in a virtual world
with whole sky display usable in VRML and QuickTime
- Beside the above mentioned analytical theories in bullet 2),
it is important to know which numerical model has been used in
the implementation. The numerical method must have been mapped
a well as possible for the period 4000 BCE to 2100 CE
(validity period).
- Being able to lock in animations on a celestial objects
(planet and/or stars)
I am using at this moment the following programs:
If people know of other (better) programs for archaeoastronomy, let me know.
The theories and their accuracy
All topics discussed in the following sections don't look at
implementations, it centres on the accuracies that can be obtained
from these theories. I assume implementations
(programs) exist that will implement these theories without
errors/bugs. Benchmarking of programs
should check this.
I have the following list on accuracies (see what inaccuracies means for local circumstances
(like altitude/azimuth)):
- Position of planets and the Sun (lx)
We can use an ephemeris that is based on VSOP82, DE200, VSOP87, DE405, DE408, etc. here with accepted
accuracy up to say 3000/4000 BCE. I understand this can be done at
a positional accuracy (Dlx)
at less than 5" (the Sun) - 14" (Mercury) - 40" (Mars) for
geocentric longitude around 4000 BCE (values of VSOP82, Bretagnon
[1986], page 7).
- Lunar position (lm)
This needs to be done using the ELP2000 models (n-dot around -25.7
+/- 0.2 "/cy2 [Pers.comm, Myles Standish, JPL, 2002]).
An accuracy for the geocentric longitude (Dlm)
of some 13' (780") at around 4000 BCE is possible in this case.
The lunar (or tidal or secular) acceleration has a similar effect
as the DT.
- DT
DT (Terrestrial Time [TT] minus
Universal Time [UT]) change the actual time that an event will
take place (and thus also the position due to rotation of the
earth). DT is not fully known for
times well before 700 BCE, so we are missing many older accurate
historical ecliptic record available (perhaps not yet found). The
DT needs to be converted if different
than (-26 "/cy2) lunar/secular
acceleration is used for the lunar position
(Morrison&Stephenson, 2012; updated formula from
McCarthy&Babcock, 1986).
ΔTconvert
= ΔTref - 0.910747 * ( ndotconvert
- ndotref) * t2
where: t = (decimalisedyear-1955.5)/100
Please add to what lunar acceleration DeltaT refers to. See
for further analyse this link.
But even for times in the near future DT
is not know to the second! See this link
where it states:
It is impossible to predict future values of DT accurately. At the beginning of AD
1999, it was 64 seconds. By AD 2100 it will probably be
between about 3 and 5 minutes.
The following set of DT formula's is important (least interdependent
and within time frame):
- Astronomical Ephemeris (1960)
- Tuckerman (1962, 1964) & Goldstine (1973)
- Stephenson & Houlden (1986)
- Borkowski (1988)
- JPL Horizons (it could be that this one will change in the
near future, due to updates of JPL Horizon)
- Stephenson: DT=35*T2-20
[Sec]
(T from 1735 CE [century]) or see table (Stephenson [1997], page 515-516).
- Stephenson & Morrison: DT=32*T2-20
[Sec]
(T
from 1820 CE [century]) or see table (Stephenson, Morrison [2004],
page
332).
A more optimized formula has been
derived by author of this website.
Because the
DT
formula's have common basis of eclipse data, the above values in
some way will flatten the inaccuracy prediction!
The accuracy of
DT
(
DDT) is around 4000 BCE some ± 250
[min], around 3000 BCE: ± 150 [min] and around 480 CE: ± 10 [min].
This accuracy is determine by half the spread between min. and
max. calculated values from above formula, which results into a
somewhat higher value than the sigma of calculated values.
In some literature (Bretagnon [
1986],
page
5) the accuracy of
DT (
DDT) is quoted around 4000 BCE at some ±
120 [min] (interpolated this gives some 85 [min] in 3000 BCE and
10 [min] in 484 CE).
Uncertainty values of Stephenson and Houlden (1986) are also
quoted
here.
In my following evaluations, I take the maximum of these two
methods; so I use the values of half the spread of calculated
values. Comments to this choice? Let
me know.
The
Hipparcos- and Tycho catalogue have a
location inaccuracy due to proper motion of resp. around 15" and
180" in declination (
Dds) and RA (
Das) for times at 4000 BCE (based on
information from Michael Perryman, ESA, Pers. Comm. [2002]).
Be aware that this inaccuracy increases for
fast-moving/close-by stars (sections 1.2, 1.5
and table 1.2.3).
- Obliquity (e)
According to Bretagnon ([1986],
page 6) the error in obliquity is around 0.1" (De)
at 4000 BCE.
- Precession of equator
According to Capitaine N. [2005]
the accuracy of the precession in longitude is very small
(considering the archaeoastronomy environment) for precession
angle looking at around 4000 BCE.
Accuracy determination in
azimuth and altitude
Using Napier's rules, VSOP82,
Monte Carlo analysis (some 2100 runs), geographical latitude of 52°
and without taking into account DT
and refraction (in case of altitude).
Values in bold are not reaching the specified accuracy range of much smaller
than 1800".
For planets
Ddx
= arctan(cos(e+De)/tan(90-Dlx))
This gives the following Ddx
for the Sun, Mercury, Mars and the Moon around 4000 BCE: 4", 12",
36" and 707"
Error on HA (Hour Angle):
Dax =
asin(sin(e+De)*sin(Dlx))
(DHAx)2= (Dax)2+ (Dlsun)2
This gives the following DHAx
for the Sun, Mercury, Mars and the Moon around 4000 BCE: 7", 7", 17"
and 316"
Using this we determine Dazix
and Daltx (Duffett-Smith [1988], page 36):
altx+Daltx=asin(sin(dx+Ddx+Press.+DPress.)*sin(f)+cos(dx+Ddx+Press.+DPress.)*cos(f)*cos(HAx+DHAx))
f = geographical latitude
azix + Dazix=acos((sin(dx+Ddx+Press.+DPress.)-sin(f)*sin(altx +Daltx))/cos(f)/cos(altx +Daltx))
The errors in azimuth and altitude vary of course due to actual
values of declination (dx) and
hour angle (HAx). When using Monte Carlo analysis, the
maximum errors found in azimuth and altitude are around the same
value as the Dlx.
So this gives the following Daltx and
Dazix for the Sun, Mercury,
Mars and the Moon around 4000 BCE: 10", 14", 40" and 800"
For stars
Dazis = (see above depending
on ds, Dds, as, Das)
Dalts = (see above depending
on ds, Dds, as, Das)
The errors in azimuth and altitude vary of course due to actual
values of declination (ds) and
hour angle (HAs). When using Monte Carlo analysis, the
errors found in azimuth and altitude are some 2-3 times bigger than
the Dds.
So this gives the following Dalts and
Dazis for stars from Hypparcos
and Tycos catelogue around 4000 BCE: 35" and 450" (the error can be
bigger, like when AH=0 and the declination has the same value as the
geographical latitude).
Accuracy's of occultation events
- Solar eclipse
Due to the DT and lunar acceleration
it seems not to be possible to predict an eclipse with an accuracy in DDT
better than a few hours local time due the lack of enough history.
Beside the local time (mostly due to DT)
also the location (mostly due to n-dot and DT)
where the eclipse will take place, can vary (if an solar eclipse
is witnessable of course also depends if the Sun is above the
horizon).
The following sensitivity analysis on solar eclipses is done:
- Have solar eclipses in remote times, e.g. the present benchmark (total eclipse on Jan. 14th,
484 CE, Athens, Greece) and an annular eclipse at 2997 BCE
(Jan. 27th). The two eclipse dates give hopefully a
picture how accuracy of DT behaves
over a period until 4000 BCE. The eclipse of 484 CE is well documented in history and the eclipse
of 2997 BCE is one of the last full eclipses that can be
calculated with DE406 (which only models until 3001 BCE).
- Determine min. and max. for DT
at that time with the help of the above mentioned DT formula's.
Calculated minimum and maximum DT [min] for 2997 BCE and 484 CE
(between brackets the formula that gave the
result):
| |
DE200
n.dot
-23.89 ["/cy2]
|
DE406
n.dot
-25.7 ["/cy2]
|
| 2997 BCE min |
1129 (5)
|
1196 (5)
|
| 2997 BCE max |
1424 (3)
|
1492 (3)
|
| 484 CE min |
71 (3)
|
77 (3)
|
| 484 CE max |
87 (5)
|
95 (1)
|
- Determine with these DT values
using the lunar acceleration parameter belonging to the
specific ephemeris; the difference in time and location of
maximum conjunction of the Moon and the Sun.
The measure of location accuracy is measured by half the angular
distance between the eclipse paths of min. and max. DT at the same Terrestrial Dynamical Time
(this distance is thus a combination of change in geographical
longitude and latitude).
In the sensitivity analysis I am not able to change the n-dot
(due to fixed ephemeris and its fix use of an n-dot),
furthermore I assume in the sensitivity analysis that the
resulting location difference due to the error in n-dot is small
compared to the resulting difference due to error in the DT.
The following computer programs are used in this analysis:
- The Digital Universe (DE200).
The location accuracy at max. eclipse is for 2997 BCE around ±
32° and for 484 CE around ± 5°.
- Eclipse animation by Andrew Sinclair
(DE406) provides more visual information (see below
animated pictures, © Andrew Sinclair, 2002).
The location accuracy at max. eclipse is for 2997 BCE around ±
57° and for 484 CE around ± 4°.
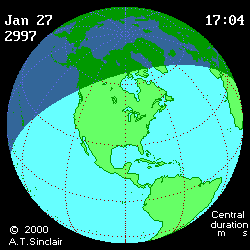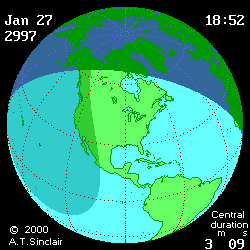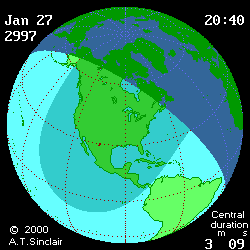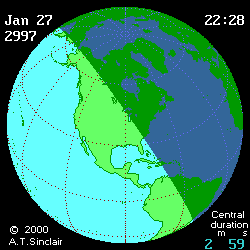
Jan 27th, 2997 BCE, DTmin=1196
[min]
|
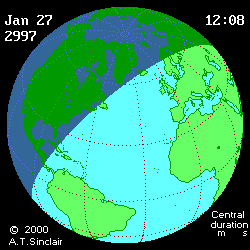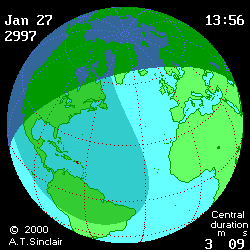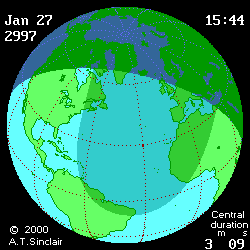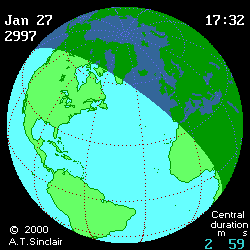
Jan 27th, 2997 BCE, DTmax=1492
[min]
|
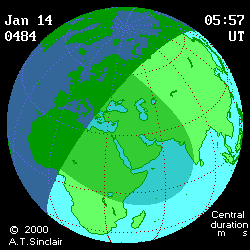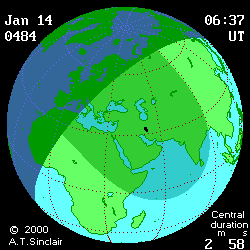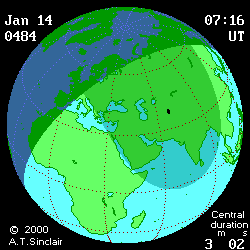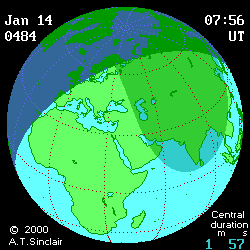 Jan 14th, 484
CE, DTmin=77
[min]
Jan 14th, 484
CE, DTmin=77
[min]
|
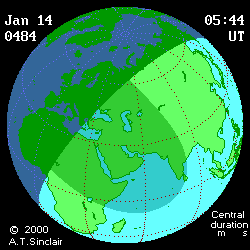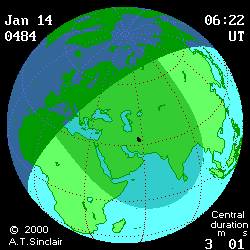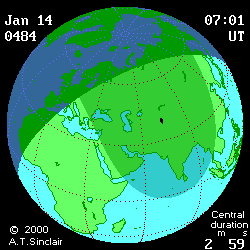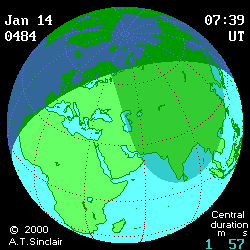
Jan 14th, 484 CE, DTmax=95 [min]
|
- Espenak's Google Map
This one can also provide comparable pictures as Andrew
Sinclair (except they are static), where one can change the
DT by changing an URL argument.
Here is a link for the Jan. 14th 484 CE eclipse with DT=77 [min] and here for DT=95 [min]
So combining the two, it looks like the max. error in location
is for 484 CE is around 5° and for 2997 BCE is around 57° (this
error is also depending on the path the eclipse takes, in the
above examples the biggest error was in the geographical
longitude)
- Occultation of moon/planet with star
This is depending on accuracy of planet/moon position and
position of the star. The lunar/planet position has already their
errors, so combining this with position of star (stellar motion)
it will become a little bit more inaccurate. One can add the
accuracy's of both together: so (Ddo)2 = (Ddx)2+(Dds)2. and (DHAo)2 = (Dax)2+(Das)2 + (2*Dlsun)2
This becomes thus for 4000 BCE:
Hipparcos/VSOP82Ddo: 19" (Mercury), 39" (Mars)
and 707" (the Moon)
Hipparcos/VSOP82DHAo: 19" (Mercury), 25" (Mars)
and 317" (the Moon)
Tyco/VSOP82 Ddo: 180" (Mercury), 184" (Mars)
and 730" (the Moon)
Tyco/VSOP82 DHAo: 180" (Mercury), 181"
(Mars) and 364" (the Moon)
Accuracy for set/rise events
Important: In the below
section the influence of DT is not
included (DT has considerable influence
on the time of the set/rise [not much on the azimuth], but this is
left for another time, perhaps I can help you in a personal e-mail:
let me know).
The error in the azimuth near the horizon is mainly determined by
parallax and refraction uncertainties (assuming an accurate altitude
of the horizon). The variation can be for parallax
between 0.9 and 1.0° (Dpar) and for
refraction a variation (1s) of 30% of
nominal value is assumed (Schaefer [2000],
page 126).
Other errors are the error (1s) in
declination of the celestial object of
0.20° for The Moon and 0.001° for The Sun (Ddx). Taking latitude at 52°, horizon apparent
altitude of 0° and around solstice/standstill limits this gives:
Dazim = 0.56° or Dazis = 0.29° (these values
are calculated with Monte Carlo analysis, some 4500 runs)
Around the equinoxes the errors are around Dazim
= 0.86° or Dazis = 0.22°
The azimuth error for the Moon and the Sun if the type of
set/rise point is not know (top or bottom limb; thus an extra
uncertainty (Dsize) between 0° and
0.52°), but no error in declination of celestial object
(so actual observation) is:
Dazim = 0.46° or Dazis = 0.38° (these values are
calculated with Monte Carlo analysis, some 4500 runs).
Around the equinoxes the errors are around Dazim
= 0.82° or Dazis = 0.29°
For solar and lunar alignments, the found errors are of the same
order as the 0.5° of Ruggles ([1999],
page
ix)
or Schaefer ([2000], page 126).
Benchmark for archaeoastronomy software
A few things should be important for benchmarking:
- determine if a computer program supports the specifications mentioned,
- determine which theories are being used
in the program,
- benchmarking them against a few known
celestial events or accepted implemented standard(s) (like
tried with JPL Ephemeris?).
At this moment several of these items are done (so looking at solar,
lunar and deltaT related issues). Future work will develop this to
more aspects of benchmarking (like for instance for star related
issues).
Possible benchmarks
The proposed benchmarks are primarily for looking at the
implementation of available formula/ephemeris into programming code
(so is its more or less about debugging;-):
- solar eclipses as discussed below, like total solar eclipse on
Jan. 14th, 484 and Aug. 11th, 1999
Will give some better idea of the implementation of DeltaT, the
lunar n-dot and the ephemeris of the moon and sun.
- conjunctions between stars and planets (perhaps Venus has a
priority because of its mention in many archaeoastronomy texts),
like Regulus conjuction with Venus on Oct. 1st, 2044.
Will give some better idea of the implementation of precession
of equator and the ephemeris of the planet.
- occultations between stars and the
moon
Will give some better idea of the implementation of precession
of equator and the ephemeris of the moon.
A good candidate for this is the observation by Timocharis, as
quoted by Ptolemy (Almagest Vii 3 H29, H30) who found "Spica
appeared exactly touching the northern point of the moon, when
as much as half an hour of the tenth hour [after sunset] had
gone by". This happened on November 9th, 283 BCE (Julian
calendar) at location 31° 11' North and 29° 50' 24" East
(Alexandria). Sun set is at 15:13 UT the day before, so ~9.5
hours later, would be ~00:45 UT. Using SkyMap Pro 9 one gets
01:08 UT, so that close...
- some related to possible alignments mentioned in literature:
- Orion stars (Zeta, Epsilon and Delta) at Giza, Eqypt in 2500
BCE (Bauval [1994])
- Reappearing sun at Maeshowe, Orkney in 2800 BCE (Reijs [1998])
- Moon at major standstill limit at Dowth, Ireland on Feb. 25th,
2983 BCE (Coffey [2000])
Total eclipse of January 14th, 484
CE.
Within the mailing list HASTRO-L (in 1996), software was discussed
and some programs were checked against the eclipse of 14 January 484
CE near Athens (38° 0' latitude, 23° 44' longitude). According to
literature this should be around that place and time.
Mr. Dearborn made an overview of the results and I (VR) have
attached new information obtained since 1996.
A general question asked in any area of research is how
dependable (accurate) are your sources (data). In
archaeoastronomy, many students depend on commercial software for
calculations of events and orientations in the distant past. Even
when you are writing your own software, it is a fairly complex
process to determine how uncertainties in the approximations of
various quantities propagate through a calculation to the answers
that you seek. In discussions on the History of Astronomy List
server (HASTRO-L), Leigh Palmer, from San Francisco State
University, proposed a test for such software. As a test of the
long term accuracy; How well it represents the eclipse of 14
January 484 (Julian Calendar)?
A. Fletcher, in Schove's (1984, p.
81) "Chronology of Eclipses and Comets 1 - 1000 AD", quotes from
Marinus' Life of the Athenian philosopher Proclus as follows:
"Portents occurred a year before his death, such as the solar
eclipse, which was so considerable that night occurred in the
daytime. For there was deep darkness and stars were seen. This
happened in Capricorn near the rising point (of the Sun)."
Totality is clearly implicit in this, but nothing in what
Fletcher actually cites identifies from where the observation of
totality was made. Fletcher reports discussion by F.K. Ginzel
(1899) and Neugebauer (1931) wherein they "argue respectively for
totality at, and only near Athens". He also cites Stephenson and
Clark (1978) as saying that "this is probably the most reliable of
all solar eclipses reported in the Classics"
Before presenting the results, we wish to reiterate that these
programs perform many functions, and that the accuracy of a
program in representing a single eclipse is at best suggestive of
its ability to represent other eclipses near that epoch. There are
sensitive geometric effects for sunrise observers, and there are
genuinely poorly known variables (like the correction between
ephemeris time and universal time; DT).
Evaluation
In the following list, the reported results are summarized. Because
individuals styles are not identical, and there is some variation in
exactly what is reported. Robert Oliver, on the performance of Dance
2.71 and Total Eclipse 1.5. Cary James sent results from the DOS
based programs, EZCosmos 3.0 and PEEP 1.02 (Planetary Event and
Eclipse (Predictor). Richard Johnson sent output from EZCosmos 4.0
and Eclipse Complete 2.0. Jim Fuchs provided input on MyStars!.
Peter Jones provided input on Cartes du Ciel. gillies macbain
provided input for Voyager. Guus Gilein provided feedback on Guide
and Redshift 5. Rob van Gent provided feebback on Redshift 3.
Vladimir Pakhomov provided input on SkyChart III. David Herald
provided input on winOccult. Sourav Maiti for SwissEph and Eclipse
Finder. Uraniustar by Rolf Straus. Victor Reijs composed the rest.
A nice
presentation
using
Google maps can be seen on Espenak's
webpage.
The below programs (in alphabetic order) have been tested. Bold
printed program names have an eclipse moment of around 5:48
+/- 0:30 (3s) UT
on Jan 14th, 484 Julian calendar (using JPL
Ephemeris and error in DT
as reference; remember that the precise
time is not known from historical accounts!). If Bold and
Italtic it is a total eclipse at Athens.
- Astro Meeuws (tested in 1996)
The program found it at 08.01 UT Jan14th, 484 CE (full eclipse) in
Athens.
- AstroSeeker
from Zephyr (date exe-file: 31/7/1989)
Some Zephyr products can find celestial objects within a skywindow
automatically.
The eclipse happened, according to the
finding-minimal-angle-between-moon-and-sun function of that
program, on: 6:06 UT.
- Carte du Ciel v2.74
Series96 from the Bureau des Longitudes between 1900 and 2100.
Plan404 based on DE404 (n-dot=-25.58 ["/cy2]) by Steve
Moshier between -3000 and +3000. ELP2000 with a truncation
for all terms smaller than 10E-8. Double-parabolic fit by
Stephenson 1986 before 1620 CE.
Has features: 1, 2 (not earlier than
3001 BCE), 3, 5, 6, 8
Total eclipse happens at 05:57 UT at Jan 14, 484 CE in Athens
- CyberSky
4.0.7 Trial
DE404 is used for the position of the sun and ELP2000-85 for the
Moon
Has features: 1, 2, 3,
5 (also some different month), 6, 8 (only read), 12
Total eclipse happens at 06:05 UT at Jan 14, 484 CE in Athens.
- Dance 2.71
The path of totality passes north of Athens. In Athens, an 84%
(partially) eclipsed sun rises at about 6:03 UT.
- ECLIPSE,
Andrew Sinclair eclipse animation (tested in 2002)
This animation uses JPL DE406 (n-dot: -25.7 ["/cy2]),
and one can input ones own DT.
Has features: 2 (not earlier than
3001 BCE), 3, 6, 8
Total eclipse at Jan 14, 484 CE in Athens
around 06:06 UT.
- Eclipse Complete 2.0 (tested in 1996)
From Athens, the maximum eclipse was about 85%, occurring at 6:40
UT, nearly an hour after sunrise.
- Espenak's eclipse predictions
(tested in 2007)
Espenak (see his eclipse web site) using the following
ephemeris: for the Sun VSOP87, for the Moon adjusted ELP2000-82
with Moon's n-dot of -25.858 ["/cy2] and DT from Morrison/Stephenson [2004]
(using Espenak's
own
polynomial description).
Has features: 2 (not earlier then
2000 BCE), 8 (one can't change DT)
Total eclipse happens at around
05:43 UT at Jan 14, 484 CE in Athens
- EZCosmos V3.0 and V4.0
The eclipse begins about 30 minutes after sunrise, reaching 95% at
7:30 UT. The altitude at this time was 15.62 degrees above the
horizon.
- Guide
8.0
Uses
VSOP87/DE200, a truncated version of the ELP-2000 for the moon and
Morrison and Stephenson for DT (1984,
n-dot around -23.8). For the stars it uses the Hipparcos, ACT and
GSC catalogues
Has features: 1, 2, 3, 8 (one can
change DT formula)
The Sun rises in eclipse (about one minute after the moon) at 5:31
UT. By 6:05 UTC the eclipse reaches approximately totality.
- IMCCE
Uses: INPOP19A (n.dot=-25.8487["/cy2]?),
Stephenson&Hohenkerk&Morrison [2016]
Has features:
2 (not earlier than 3001 BCE), 3
Partial eclipse (0.99)
happens in Athens at around 05:44 UT (at Sun rise)
on Jan 14, 484 CE
- JPL HORIZON
Ephemeris Version 3.15
The is a web based planetarium program (based on DE405/DE406
(n-dot: –25.7 ["/cy2]) and their own DT formula related to Stephenson [1997]
(n-dot: -25.7 ["/cy2])) (Pers. comm. Giorgini [2005]).
Has features: 1 (no Milky Way
contour), 2 (not earlier than 3001 BCE), 3
Total eclipse happens at 5:48 UT on Jan 14th, 484 CE in Athens
- Mobile Panjika
(checked Dec. 2007)
Here is another high precise archaeoastronomy software can for
mobile phone calculate eclipse timings accurately from 3000 BCE
to 3000 CE. The heart is Swiss Ephemeris, but ported for mobile
phones and the value used for the Moon's n-dot is -25.858
["/cy2] and DT from
Morrison/Stephenson [2004]
(using Espenak's
polynomal description).
The time of max eclipse at Athens (14 jan 484 CE): 05:43 UT
- Moon Calculator 5.2
Gives a clear view of the phases and visibility of the moon.
- MyStars! 2.7
Eclipse happens at 05:38 UT at Jan 14, 484 CE in Athens, 98% and
the Sun 1 degree below horizon
- PEEP V1.02
The eclipse was total at 5:56 UT, just after sunrise.
- Planetary, Lunar and Stellar
Visibility 3.1.0
It uses Chapront-Touzé & Chapront (1991) for DT.
The eclipse at Athens happens at 6:03 UT on Jan 14th, 484 CE in
Athens (around 100% eclipse)
- RedShift 5
Maximum eclipse (no total) happens at 06.38, sun 0.5 degrees below
horizon. It shows just the tiniest smidgen short of totality at
Athens with the Sun and the Moon just in the process of
rising.
- RedShift
3
Maximum eclipse at 5:48 UT on Jan 14th, 484 CE in Athens, on the
verge of a total eclipse
- SkyGlobe 4.0
Has features: 1, 2 (except horizon
dip, change in obliquity), 5 (lunar synodic and day), 6
Eclipse happens at 11:05 UT on Jan 14th, 484 CE in Athens (around
50% eclipse)
- SkyMap Pro 10
This program is based on VSOP87, ELP2000-82B and Stephenson &
Houlden (1986) (is under study by author (pers. comm Marriott
[2004]) and n-dot =-26 ["/cy2] adapted to ELP2000-82B.
Has features: 1, 2 (except horizon
dip), 3, 7 (manual with Annotation: camera frame), 8
Eclipse happens at 6:05 UT on Jan 14th, 484 CE in Athens (almost
total eclipse)
- SkyChart III 3.2.3
Has features: 1, 2, 6, 7, 8, 9
The partially eclipse happened, according to the
finding-minimum-angular-separation function of that program,
6:30 UT on Jan 14th, 484 CE in Athens
- Sky View Café V4.1.8
Java based
program. Stand alone version has full VSOP87 and ELP2000-82
precision and Chapront, Chapront-Touzé & Francou (1997) for DT.
Has features: 1 (no Milky Way
contour), 2 (except horizon dip), 3, 5 (some options)
Eclipse happens at 5:42 UT on Jan 14th, 484 CE in Athens, Greece
- StarCalc 5.72
Eclipse happens at 6:06 UT on Jan 14th, 484 CE in Athens, Greece
- Starry
Night
Pro 4.x
It uses use for the Moon, the Sun and the Earth position Meeus
(VSOP87) and Chapront moon (ELP2000-82). Uses their own DT formula (DT
can be viewed in the Pro-version of the program), but planning to
use Stephenson in the near future (Pers. comm. Braganca [2003]).
It shows the eclipse is at 6:02 UT at an apparent altitude of 2°
19'.
- Stellarium
(0.20.4)
Uses DE431 (Moon's n-dot is -25.8 ["/cy2]) or
VSOP87&ELP2000-82B (Moon's n-dot is -23.8946 ["/cy2])
and DeltaT
(Stephenson&Hohenkerk&Morrison [2016] or Reijs
2006)
An almost total eclipse happens at 6:16 UT on Jan 14th, 484 CE
in Athens, Greece (just below the horizon and using
VSOP87&ELP2000-82B).
- SunHeight
(checked on Jan. 7th, 2005)
Discussing with author about results gotten for the eclipse (looks
far off) and present times. The author is debugging this now due
to my feedback.
- Swisseph 2.10.1
DeltaT from
Stephenson&Hohenkerk&Morrison [2016]
and JPL DE431 (n-dot=-25.8 ["/cy2] or Moshier (based on DE404,
n-dot=-25.58 ["/cy2]) for Sun and Moon ephemeris.
Has features: 1, 2, 3
Parial eclipse happens at 5:46:40 UT (at Sun rise) at Athens on
14 Jan. 484 CE (using Moshier)
- The Digital Universe V2.0
This program (based on DE200, ELP2000-85 (n-dot=-23.8947 ["/cy2])
and Stephenson & Houlden (1986; n-dot: -26 ["/cy2]))
looks
to
have almost all of the wanted features. It is only available for
Mac at this moment.
Has features: 1 (in demo version: no
stars or Milky Way), 2, 3, 5, 6, 8
It could be that features 4 and 7
will perhaps also be implemented (Pers. comm. Charrois [2002]).
Total eclipse happens at 5:57 UT at Jan 14, 484 CE in Athens (the
full eclipse happens at 6:06 UT when using an n-dot of -23.89)
- TheSky6
Astronomical algorithms from Jean Meeus (VSOP 87???).
Has features: 1, 5, 6, 8 (one can't
change DT), 9???
This planetarium program show the Sun eclipsed on 14 Jan. 484 CE
at 7:30 UTC (DT = 78.5 [min]). The DT
looks to be oke, so something else in the ephemeris must to be
wrong.
- Total Eclipse V1.5
A near total eclipse (99.4%) occurs at 5:44 UT. At this time the
Sun would appear to be rising on a level horizon (altitude -0.6)
The path of totality north slightly of Athens.
- Uraniastar 1.1
Lunar positions on
the basis of Ernest Brown’s lunar theory in a slightly
abridged version of Jean Meeus.
Partial eclipse (0.992)
of 484 CE, January 14
UT 5:45.
- Voyager III
3.21 Mac
It uses VSOP87, ELP2000-82B and Stephenson & Houlden (1986)
for DT.
The Sun and The Moon have almost the same coordinates at 5:57 UT
Athens Jan. 14th 484 CE
- winOccult 3.1
Program build around occultations of the moon. The calculation
is based on a deltaT of 79 [min] (using Stephenson & Houlden
[1986]). Sun: VSOP - which is a fit to DE200. Moon: Chapront
ELP2000-82B - also a fit to DE200.
Has features: 1, 2, 3, 8 (but not in eclipse module!)
Maximum eclipse at Athens at 5:57 UT, at an altitude of 1
degree. The eclipse is not total, with a magnitude of .968.
- Your
Sky (checked Dec. 22, 2004)
The max. eclipse coverage is at 8:10 UT. But it is certainly not
full.
- Others?
A good link on planetarium programs is here (MacOS, MS Windows, DOS, X, Palm, OS/2
WARP).
Let me know if you tested one! Investigating
the precision of a tool is fundamental to basic research, and no
numerical simulation should be considered to be absolutely accurate.
The ground track of eclipses, particularly near the limb of the
earth, are sensitively dependent on the precise value of a number of
difficult to determine variables. So, it is understandable how a
program may do well on one eclipse and not so well on another of the
same epoch.
The testing discussed here is a good beginning, but confidence
should be based on more that one test. In addition, tests should
be collected on events other than eclipses.
Acknowledgements
I would like to thank the following people for their help and
constructive feedback: Dan Charrois, David Dearborn, Robert van
Gent, Michael Gorodetsky, Paul Hirose, Steven Hope, Michael
Perryman, Tom Peters, Thomas Schmidt, Andrew Sinclair, Myles
Standish and all the people who provided feedback on specific
computer programs. Any remaining errors in methodology or results
are my responsibility of course!!! If you want to provide
constructive feedback, let me know.
Disclaimer and Copyright
 Home
Home Up
Up Search
Search Mail
Mail
Last content related changes: Aug. 23, 2002



