HomeUpSearchMail
NEW

---

Assumptions on calculations of limiting visual magnitude, extinction angle and shadow casting

• two B_sky models are defined:
• Arch. XI
Archaeoastronomy XI [1993]. This model is not described anymore in the latest article of Schaefer [2000], so I assume this one is not valid for my purposes. This model is implemented by Ben Sugerman in JavaScript
• The dimensions of the B_x in Arch XI  are in [nL].
• Arch XV (used by my calculations)
Archaeoastronomy XV [2000] comparable with Sky and Telescope [1998] (BASIC program provided by B. Schaefer and JavaScript of Bogan).
• Some typo's in Arch XV are discussed here.
• In Arch XV the V (Visual magnitude) is the only option used of the UBVRI magnitudes, so that photometric formula (eye depending) can be used.
The two B_sky models behave quite differently. The differences are (these have no influence when the sky is really dark):
• It looks that in Arch XI one argument of the phase function f _(r), mentioned in Arch XV, is not used. Deleting this argument  (440000*(1-10^-0.4kX)) in Arch XV one gets almost the same results.
• B_night (in [nL]) in both models are comparable (although the value of B₀ in Arch XI is unknown, taken as 180 by me).
• B_moon (in [nL]) in Arch XI is always smaller than in Arch XV (some factor of 54 at 1° (r_moon is 1°) and going down to a factor of 1 at 45° apparent altitude (r_moon is 45°)).
• B_twi (in [nL]) is in Arch XI always bigger than B_day until apparent altitude is lower than -14° (azi_sun-azi_look around 180°)
• B_day (in [nL]) in Arch XI is always smaller than in Arch XV (some factor of 54 at 1° (r_sun is 1°) and going down to a factor of 1 at 45° apparent altitude (r_sun is 45°)).
Is Arch XI indeed not valid anymore? In the meantime Arch XV is implemented.
• Is it allowed to use Dm(Z)=k_R*X_e(Z)+k_OZ*X_L(Z)+etc. (8b) for greater accuracy instead of Dm(Z)=kX(Z) (8a) in the B_x-formula's of Schaefer [2000]? In my calculations this (8b) is being used.
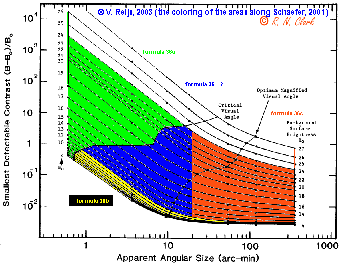
• What formula is needed for (log(B)<6 and Q_CVA<z<~20') (the blue area)? In the below graph the approximate formula-boundaries provided by Schaefer [1993] can be seen (the black lines are the data of Blackwell [1946]):

• A possible solution is using the max(formula (36a),formula (36c)): called Schaefer+ (the dots are the data of Blackwell [1946]):

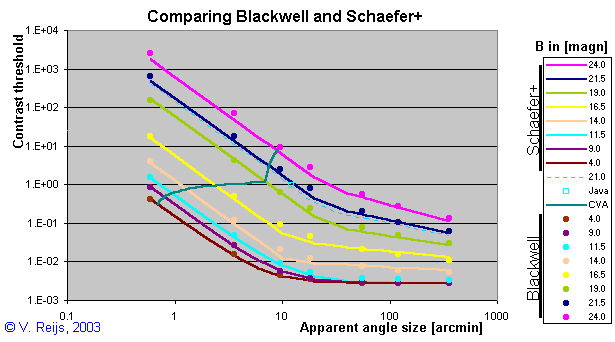
The colored lines are calculated using the max(formula(36a),formula(36c))
The dots are the Blackwell data.
• another alternative: linearly interpolate between (36c) and (36a) for apparent angle sizes between 10' and 100' (idea of Thomas Schmidt).
• my JavaScript has the Blackwell [1946] table (the dots in the above picture) incorporated using interpolation. This though gives in most cases a higher contrast threshold than of Schaefer.
• The conversion from [erg/sec/cm²/mm/arcsec²] to [nL] is used.
This conversion is build up as follows (see also this convertor link):
nL TO erg / second centimeter² steradian = 3.183*10^-3 lumen / watt
Taking 1 lumen = 1.464*10^-3 watt as the normalized value (for photopic vision at 0.555 mm):
1 [nL] = 4.660*10^-6 / "Integral over visible light of normalized Luminosity curve" [erg/sec/cm²/mm/steradian]
For 1 arcsec² = 2.35*10^-11 steradian
1 [nL] = 1.095*10^-16 / "Integral over visible light of normalized Luminosity curve" [erg/sec/cm²/mm/arcsec²]
The "Integral over visual light of normalized Luminosity curve" is 0.242 [mm] (scotopic vision) or  0.107 [mm] (photopic vision) over visual light of 0.36 mm to 0.83 mm.
So the conversion value is 1.02*10^-15 for photopic vision (B>10^3.17 [nL]) and 4.48*10^-16 for scotopic vision (B<10^3.17 [nL]) (the BASIC program has 1.11*10^-15 in all cases).
It could be that something needs to be changed in the code to reflect the boundary of photopic/scotopic vision.
This issue is solved due to the formula for the threshold, which is different for above and below B<10^3.17 [nL].
• Just some other small additions/changes:
• How to derive the atmospheric extinction coefficient (k_x) from the atmospheric absorption coefficient (ß_x) can be seen here.
• The airmass has been made dependent of the air pressure.
  
• changed k_OZ, k_a and k_R when night vision is effective (sun lower than start of astronomical twilight (Vistas in Astronomy, page 343).
• ±s_aW=0.01±0.4*(k_a+k_W) has been used to get the skewedness of the s_aW (as defined in Arch XI (6b)).
• changed B_night in such a way that it is in pace with sun-spot cycle (start: 1990.33 and a period: 11.1 year).
• increased contrast threshold (increased log(contrast) with 0.2) so that not 50% but 90% certainty exists in viewing the shadow difference (Blackwell [1946]).
• included that from apparent observational altitude is <10°, B_night is kept constant (Vistas in Astronomy, page 343).
• age of person has been included (using Garstang [2000]).
  
• the Moon's magnitude is made dependant on it's distance from earth.
• Added the concept of the sky window,
• Added model to calculate the visibility of the moon on the horizon (for lunar standstill event in 2006),  moon's shadow inside an enclosure (like a passage monument) and heliacal events.
  
• Excel Add-in functions have been made.
  

Disclaimer and Copyright
HomeUpSearchMail