NEW
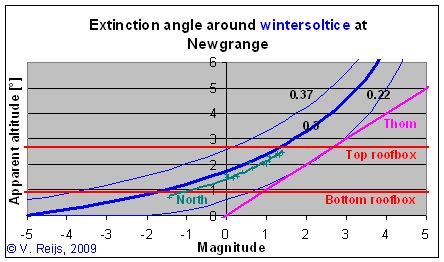
The extinction angle determines at what apparent altitude a
celestial body becomes visible. The above picture has been made
with information from Bradley Schaefer [2000]. A JavaScript and Excel Add-in Visual Basic
(VB) program is available. The assumptions used within the
Schaefer implementation can be seen
here.
The thick blue line (winter solstice at average present
Irish conditions: 80%, 5° C and AEC=0.3) is the extinction angle
depending on the Magnitude of the celestial body (moon and sun as
much as possible under horizon). The thin lines provide the 1s boundaries (0.07).
The green-blue crosses are sightings in south England under
favorable conditions from North [1996,
page 34] (which compares to an atmospheric extinction coefficient
of 0.3 [-] at 10% RH). And the pink line is the rule of thumb from
Thom [1976, page 15].
The red lines are the apparent altitudes which are visible through
the roof box of Newgrange.
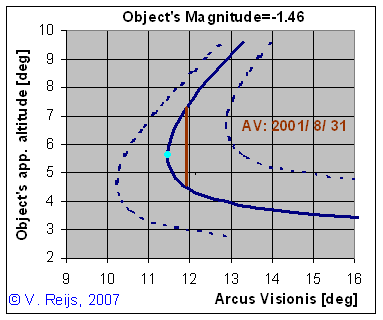
An example: In winter time Sirius (the brightest star:
Magnitude -1.46) is visible when it is at an apparent altitude
of higher than appr. 1°.
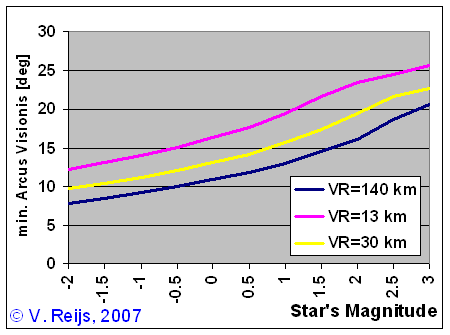
The minimum Topocentric AV is the smallest unrefracted angle
difference between the star (in general: celestial object) and the
Sun while the celestial object is just visible on the heliacal
(rise/set) day.
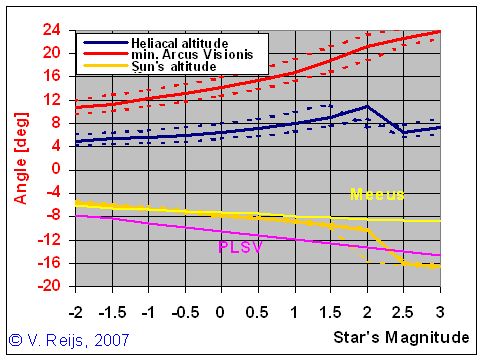
In the below picture one can see the minimum Topocentric AV as a
function of the object's Magnitude (same
conditions as above are used and variable atmospheric extinction
coefficient).
| Object | Ptolemy Handy Tables |
Schoch |
Meeus [1997] |
Reijs* |
|||||||
| hr/hs |
ar/cs |
hr |
ar |
cs |
hs |
hr/hs | hr |
ar |
cs |
hs |
|
| Saturn |
13 |
13 |
10 |
10 |
13.5 |
10.0 |
9.6 |
12.8 |
|||
| Jupiter |
9 |
9.3 |
7.4 |
8 |
9.7 |
6.4 |
6.0 |
9.8 |
|||
| Mars |
14.5 |
14.5 |
13.2 |
11 |
14.0 |
7.6 |
7.0 |
16.0 |
|||
| Venus |
5 |
7 |
5.7 |
6 |
6 |
5.2 |
6 |
6.9 |
7.6 |
7.3 |
6.4 |
| Mercury |
12 |
13 |
9.5 |
10.5 |
11 |
- |
14.8 |
10.2 |
11.3 |
16.1 |
|
| Middle astronomical year |
Reijs' results [Day]/[Solar day] |
Ingham's results [Solar day] Table 3 |
| -3498 |
365.25000/365.25042 |
365.25051 |
| -2043 |
365.25035/365.25066 |
365.25085 |
| -590 |
365.25104/365.25124 |
365.25126 |
| 861 |
365.25190/365.25199 |
365.25181 |
|
|
|
| Sun | -27 |
| Moon | -13 |
| Venus | -4.7 |
| Mars | -2.9 |
| Jupiter | -2.8 |
| Mercury | -1.9 |
| Saturn |
0.7 |
| Uranus | 5.5 |
| Neptune | 7.7 |
| Pluto | 13 |
The casting of shadows depends on the brightness of the celestial object and the amount of background light from other celestial objects.
From literature (Waugh, [1973, page
167]) it looks like that the moon still casts a shadows in open
air when its phase is 7 days before (or after) full moon. Its
magnitude is then around -10.
I have experience that with full moon at an apparent altitude of 1.5° and the
sun at nautical twilight, I could discern a shadow in closed
duct, aligned to the moon. If people have comparable experience,
please let me know.
I got an e-mail reaction that the Venus (magn
-4) shadow has been seen quiet faintly. This was at an ideal
location: Apache Point, about 2.7 km above sea level in the
mountains of New Mexico and the sun had set more than an hour
earlier.
Under good conditions, of the planets only the Moon, Venus and
the Sun can cast a shadow, and of the stars: non.
I would like to thank the following people for their help
and constructive feedback: Ari Belenkiy, Rumen Kolev, Dieter
Koch, Jim Lowdermilk, Keith Pickering, Bradley
Schaefer, Thomas Schmidt and all other unmentioned people. Any
remaining errors in methodology or results are my responsibility
of course!!! If you want to provide constructive feedback, let me know.