HomeUpSearchMail
NEW

Parametrisation the height-temperature profiles

• CASES99Bench, this one is used as reference profile
  HT profiles (between 0.23m and 58.1m) during Sunrise and Sunset based on Stephen McCluskey's derived from the CASES99 study on 18 dates (October 1999).
  
• CASES99Approx
  Each of the above HT CASES99Bench profiles, have been approximated by using two curves and one point:
  

1. Low height range of CASES99Bench (blue dots)
   A logarithmic of quadratic curve (depending which has the maximum goodness of fit [R²/coefficient of determination closest to 1]).
   
2. High height range of CASES99Bench (orange dots)
   A linear curve (showing a lapse rate).
   The CASES99 HT profiles look to have above the surface layer an average lapse rate (up to 58.1m) of 0.036K/m for Sunrises and 0.009K/m for Sunsets. This behavior is indeed expected due to the well developed NBL of the night.
   
3. A surface layer point
   The surface layer point between the two ranges (in below graph at 10m) was optimised to fit an overall smooth result (gray dots).
   There is no significant difference in the height of the surface layer: 18m for Sunrises and 17m for Sunsets. One would expect a higher surface layer for Sunrise due to the well developed NBL of the night.

• MUSA76
  The average surface layer over all CASES99 HT profiles was derived (around 18m) and the average lapse rate (between 0.23m and 18.5m) of each CASES99 HT profiles. These were used in MUSA76 profile (van der Werf, 2003).
• CASES99OneStep
  A profile that has a constant lapse rate and the temperature at 0.23m, 10m and 58.1m are the same as at each CASES99Bench. For levelling refraction the Near and Distant temperature should determine the refraction. This profile is not used for astronomical refraction (as Distant has no real relevance for refraction)
  
• AstroRefract_ATS, LevelRefract_VR and TerrestRefract_VR approximation formula
  The average lapse rate of each CASES99 HT profiles was provided to formula (1) for astronomical refraction (between 0.23m and 58.1m), formula (2) for levelling refraction (between 58.1m and 10m) and the formula (5) for terrestrial refraction (between 0.23m and 58.1m).

Looking at Astronomical refraction

The eye is at 1.65m height (Near). All profiles are extended up to 85km with MUSA76 profile (average temperature gradient=0.0065K/m between 58.1m and H_r at -56.5C [around 11km]).

Results

• CASES99Approx
  The CASES99Approx maps very well (as expected) on the CASES99Bench (within 2%)
  
• MUSA76
  The MUSA76 maps reasonable well on the CASES99Bench (within 10%).
• AstroRefract_ATS formula
  The AstroRefract_ATS maps least of all on the CASES99Bench (between 0 and 15%), because the formula does not incorporate a dependency on lapse rate.
  

Looking at levelling refraction

The eye is at 58.1m (Near) and the vast level surface is at 10m (Distant). If using a vast level surface at 1.65m, the CASES99 profiles give refractions that make the ground go high up around zero (AZAAR) and negative (NAAR) apparent altitudes. because the near ground lapse rate (between 0.23 and 0.63m) is lower than -0.11K/m (see below picture). So a Fata Morgana (superior mirage) is what happens.

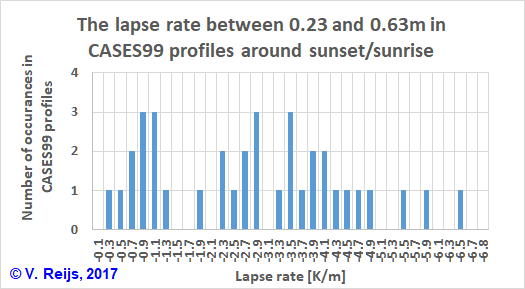
To get enough data to compare, the vast level surface has been put on 10m and some profile change was made to MUSA76:

• MUSA76
  The surface layer was set at 1000m and the average lapse rate (between 10m and 58.1m) of each CASES99 HT profiles were used in MUSA76 profile (van der Werf, 2003).

Results

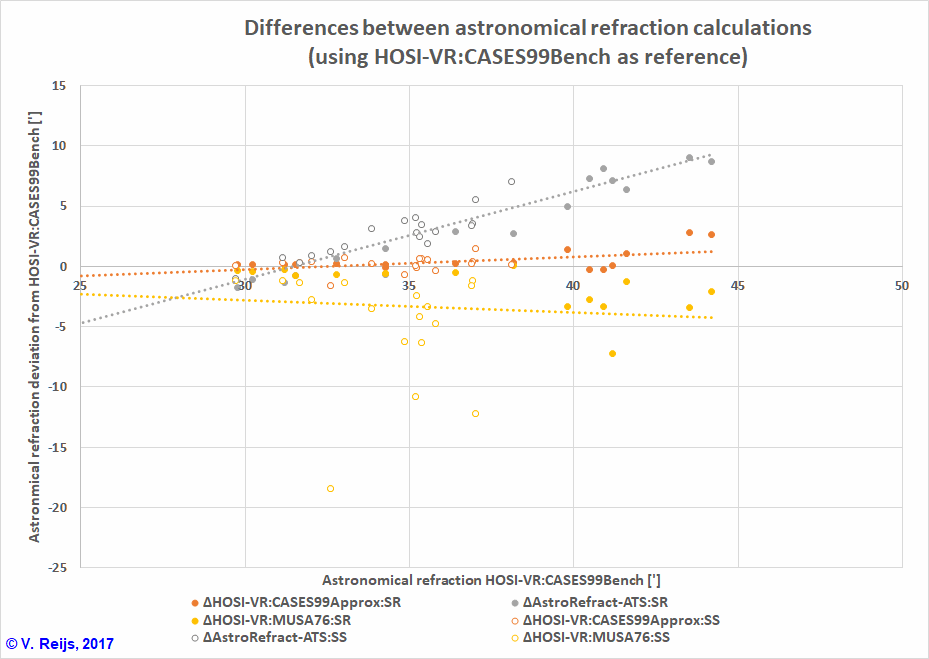
Below one can see the differences (in arcsec) with the reference data (CASES99Bench):

• CASES99OneStep
  The CASES99OneStep maps very well (as expected) on the CASES99Bench (within 2%). It shows again that for levelling refraction the Near and Distant temperature are more important than the (detailed) height-temperature profile.
  
• LevelRefract_VR formula
  The LevelRefract_VR maps on average quite well on the CASES99Bench (between 0 and 15%).
• CASES99Approx
  The CASES99Approx maps reasonable well (as expected) on the CASES99Bench (within 10%)
• MUSA76
  The MUSA76 maps reasonable well on the CASES99Bench (within 10%)

Looking at terrestrial refraction

Results

• CASES99Approx
  The CASES99Approx maps on average reasonable well (as expected) on the CASES99Bench (between 0 and 15%)
• TerrestRefract_VR formula
  The TerrestRefract_VR maps on average poorly on the CASES99Bench (between 0 and 50%)
• CASES99OneStep
  The CASES99OneStep maps on average poorly on the CASES99Bench (between 0 and 70%). It shows again that for terrestrial refraction the Near and Distant temperature are not good indicators for the refraction.
• MUSA76
  The MUSA76 maps the least of all on the CASES99Bench (between 0 and 80%)

Observations

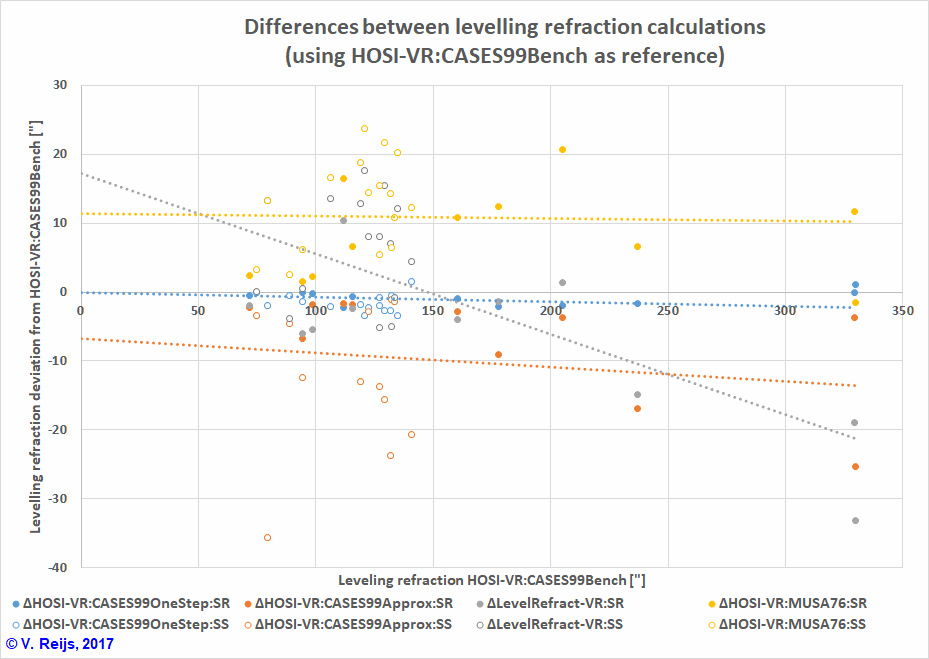
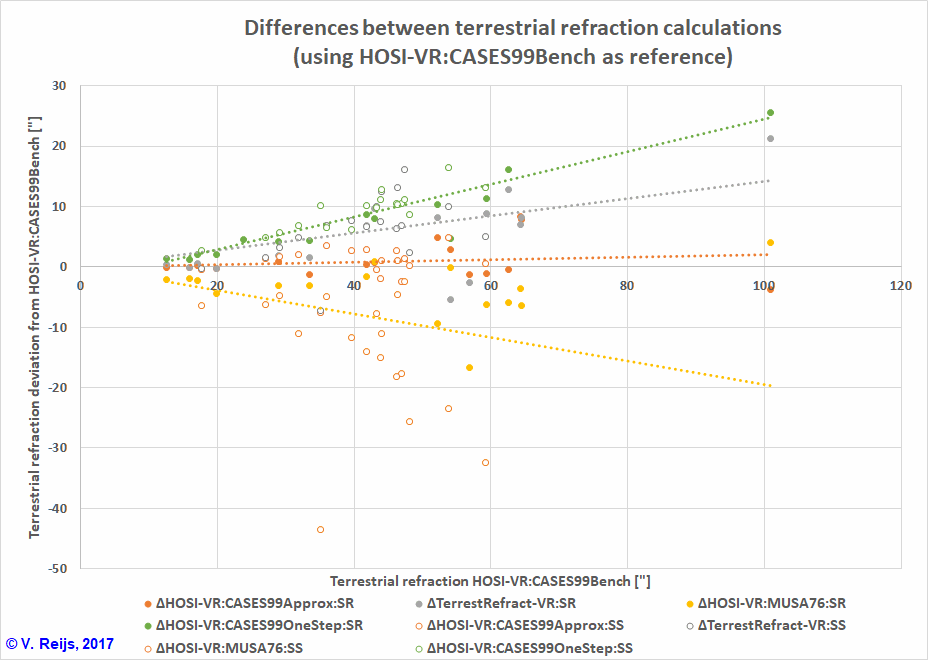
If we check the differences from the CASES99Bench results, we get the following overview (between bracket the average value):

<Green means the best mapping profile>
<Red means the on average worse mapping profile>

CASES99Approx is the best solution; except for levelling refraction where it is CASES99OneStep. MUSA76 looks not to be the best method.
The Formula perform in an average way.
All of these methods (including CASES99Bench) have the drawback that for former times (like in archaeoatronomy) the parameters (like [approximated] HT profile, Near&Distant temperature or average lapse rate) are unknown and very difficult to predict.
So perhaps we need to try our best to predict the parameters (by knowing the events [rise/set], the location, a general idea of the HT profile and the temperatures), and this might give the accuracy quoted in the above table in the row Maximum of above for the different refractions. This is not that far from the astronomical refraction variation seen in this web page. (around 5' variation of the astronomical refraction at AppAlt=9')

References

Acknowledgements

Disclaimer and Copyright
HomeUpSearchMail