Using the above mentioned
Profiler: Each of the layers at a certain time of
the day (for land environment) gets additional
parameters to define the potential temperature (Θ) and
its behavior inside that layer. The functions which at
this moment implemented are:
- a step-ish function; it can simulate (a),
(b) and (c) in the above
picture: the function is defined by the step
size, the layer depth, the lapse rate or temperature
strength
- a polynomial function; this can simulate (c) and
(d) in the above
picture: the function is defined by the order
(from 0 to n; n can be any positive real number),
the layer depth, the lapse rate or temperature
strength.
- an exponential function, this can simulate (e) in
the above
picture: the function is defined by the size
of the tail-off, the layer depth, the lapse rate or
temperature strength.
- other functions or data sets can be added.
- The Profiler incorporates a user defined
temperature, pressure and lapse rate table (to
provide for a diurnal effect on temperature related
aspects).
- The left picture is generated by the Profiler: it
can be compared to the above
development of the profiles from R. Stull.
|
The horizontal lines
at the top means that above that the free atmosphere
should start (not incorporated in the picture). The
legend number [4 to 14] means the LST time of day. The
temperature at Height=0 and the lapse rate are
depending on time [LST].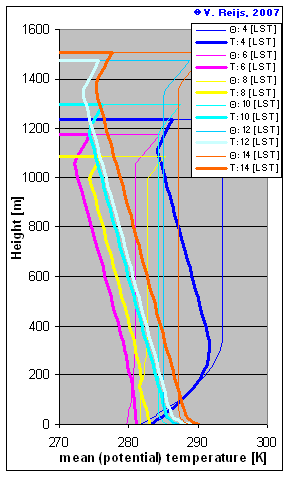 |
 Home
Home Up
Up Search
Search Mail
Mail  Home
Home Up
Up Search
Search Mail
Mail