Mail
NEW

Some remarks on the DHM formula

Some remarks on the DHM formula by Victor Reijs is licensed under CC BY-NC-SA 4.0

Introduction

On this web page the DHM formula will be discussed. It will look at the background and a possible verification and optimisations of the formula.

Several questions are outstanding, see below purple text. If you have input, please let me know.

Background

According to De Hollandsche Molen (DHM) windmolenbiotoop formula (which heavily uses the article presented by Beljaars [1979]. [Werkgroep Molenbiotoop, 1982, page 24]) the maximum obstacle height (H_DHM) (rekening houdende dat de windsnelheid tot maximaal 95% mag verlagen [e.g. windenergie verlaging tot 86%]):
H_DHM=x/n + c*z

H_DHM: hoogte van een lijn vormig obstakel [m]
x: afstand tussen obstakel en molen [m]
z: hoogte askop [m]
n=50 (bij z_0m=1m en 95% windsnelheid verlaging); this could be called: Wake decay rate
c=0.2 (bij 95% windsnelheid verlaging van 86% energie verlaging)

The conditions are:

An ABL looks to be use due to logarithmic wind speeds in many graphs (e.g. Beljaars [1979, page 40 and Fig. 4.8] and z_0m being an explicit parameter.
The windspeed at shaft height is taken as reference for energy calculations [Beljaars, 1979, page 8].
The formula is derived by lineair interpolation when determining the power loss over the sails' span. The efffect of the logarithmic ABL is linearilise over the sail span (Figure A.1).
Only power loss of 95% and 90% are part of the DHM formula (Beljaars has a larger range).
It assumes no obstacles within 100m.
c is relatively independent on H/z_0m.
A thin long (slightly porous) obstacle with height H has been used (Beljaars, page 22) to verify Townsend's model. The thin long obstacle needs to be quite distinct in height from the rest.
Beside that an extra roughness over a larger area has been evaluated. While that might be more realistic, the thin long obstacle provides a better approach when looking at both wind speed and induced turbulence intensity.
The real height of the object is input parameter (the effective height is part of the exprimental results, model aka formula, if a fence heightens the profile in the same way as a building!).
Remark: check if the effective heightening of fence and house-block are simular.
The tables/graphs/formula are only valid for distance x longer than the cavity boundary (x > 15*H) (Beljaars, page 12); and H larger than 10*z_0m (Beljaars, page 15).
Beljaars' boundary migth be related to: The roughness length (z_0m) dictates the roughness height (k_s) at 10* z_0m, thus below that roughness height the formula is not accurate.
H should not be larger than 2.5*z (for 90%) or 3.5*z (for 95%) (Beljaars, Figure 5.1).
The model [Townsend, 1965] has been verify and optimised by Beljaars with a porous fence ([Nägeli, 1946] optical porosity between 15% and 20%).
Below picture also includes a comparison with a CFD simulation of a porous medium (Forchheimer coefficient=12.8; colored curves).
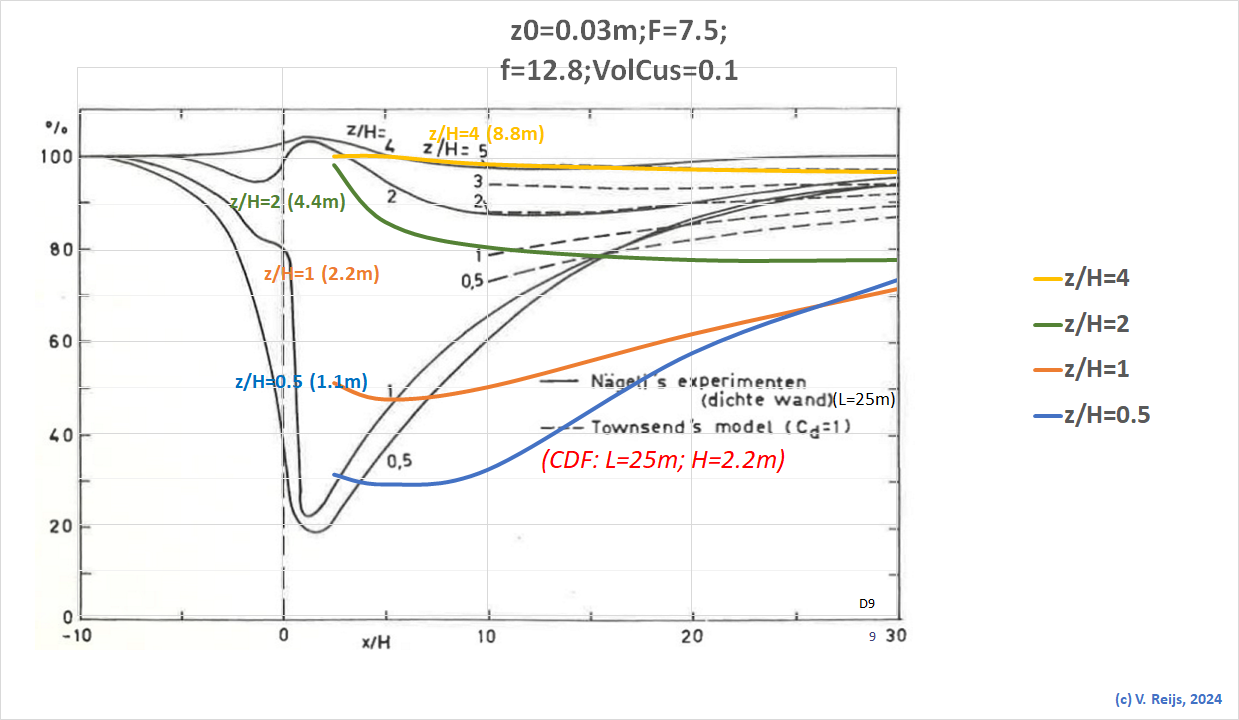
So DHM formula is based on a model adjusted to match experimental in-vivo results of a slightly porous obstacle.
Trees are not explicitly investigated, but the DHM formula itself does not disciminated between buildings and trees (bebouwing- en beplantingshoogte) [Werkgroep Molenbiotoop, 1982, page 24]
The functionality of DHM workflow is:

Model the environment with one obstacles per direction
Calculate the H_DHM
Determine if height obstacle is heigher than H_DHM,
If the obstacle is higher, the obstacle migth casue a problem, otherwise it looks ok
Do this for every direction wanted.

Some typos/errors

A few typos/errors look to exist in the document of Werkrgoep Molenbiotoop [1982]:

page 25
replace ''1/n is de richtingscoefficent van deze lijnstukken." with "n is het snijpunt van deze lijnstukken met de horizontale as.".
page 25
In Afb. 12 the coefficient c is given. These values are rounded to one decimal. If included 2 decimals we would get '0.25' and '0.16'. How c is related to speed loss can be found here.
page 25
replace 'Bovendien is de term c.z vaak groter dan x/n' with 'Bovendien is de term c.z vaak kleiner dan x/n'.
page 25
The statement 'globale benadering van n volstaan' (a global approach for n is sufficient) does not look to be correct. As n is depending on H/z_0m, it is better to keep this dependency in the formula. The problem though is that it becomes an iterative process to derive the H (that might also be the reason why they used a simpler approach). The evaluation of introducing this dependency will be done in the next section.
page 26
replace 'H = 550/80 x 0,2.12' with 'H = 550/80 + 0,2.12'
page 26
The derivation for the validity of the DTM formula is valid (x>15H: looking at cavity boundary). But there is another aspect that determines the validity of the DHM formula and that is the non-linear dependency of z/H and x/H (see Afb. 11), which is assumed linear when just using the c and n as defined in DHM formula. Better is to determine the range of real linear part in Afb. 11 and deriving from that the validity of the DHM formula. This will also be evaluated in the next section.
Beljaars zegt [1979, page 42] dat de gemeten wind door Nägeli zich sneller hersteld doordat het scherm relatief kort is (25m).
Remark: Dit komt eerder doordat het Nägeli scherm poreus is.

Most of the above points don't change the formula, except for points 4 and 6.

Optimisation of the DTM formula

This secion is heavily based on the results of Beljaar (the DHM formula uses Beljaars as its basis, except a few simplifications are introduced in this DHM formula). This section will analyse these simplifications.

Determing H through new c and n

Still using the DTM formula H =x/n + c.z (x > 15H). But we don't use a constant c and n, but use logarithmic formulas depending on H/z_o derived from the curves in Afb. 11 [Werkrgoep Molenbiotoop, 1982] (for 95% and 90&% speed factors) and Table 4.5 to 4.8 [Beljaars, 1979] (for 85%).
c and n
dependent of x/h

Remember this is though a approximation and migth only work for low speed losses. More analysis of Beljaars tables, Nägeli would be needed.

Using this, we can calculate the H for different distances x. from the ground-sailer.
The DHM formula values (orange curves) and the Beljaars graphs (blue curves) can be seen below.
The thin curves are for a 95% speed factor, the somewhat thicker curves for 90% and the double curves for 85%.
The dashed curves are for z_0m=0.03m while the continuous curves are for z_0m=1m.
De H1:30 and H1:100 curves are applied to the distance between the obstacle and the mill.

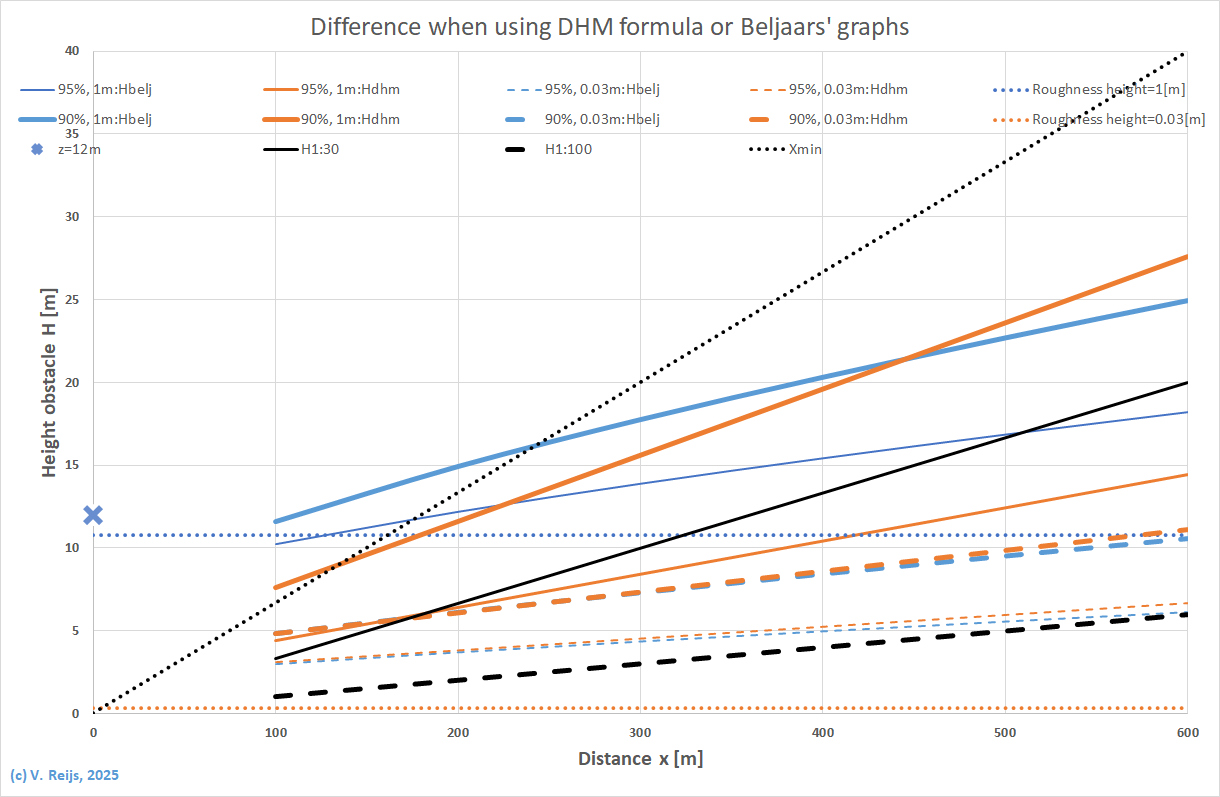
Comparing DHM and Beljaars tables

For speed factor of 80% regardless of z_0m; Beljaars' allowable obstacle heights (H) are some 20% higher then DHM's. For higher speed factors and low z_0m (0.03m); Beljaars' and DHM's results are quite close.
For high z_0m (=1m); Beljaars' allowable obstacle heights are higher then computed by DHM.
Remember the boundaries of Roughness height (k_s: above colored dotted line) and X_min (>15*H: below black dotted line).
So the larger z_0m, the lower the speed factor or the smaller x; the larger the absolute difference between Beljaars and DHM becomes.

Speed loss and speed factor

When looking at a c (called coefficient by Werkgroep Molenbiotoop [1982, page 25]) with 1 decimal a liniear formula is ok-ish: speedloss ~ c/3 and speedfactor ~ 1 - c/3
<this formula is an approximation, assuming an H/z_0m between 15 and 60>

A rewrite of the DHM formule

So one could rewrite DHM formula:

H=x/n(H/z_o ) + c*z
c = 3*(1-SpeedFactor)
H=x/n(H/z_o ) + 3*(1-SpeedFactor)*z

SpeedFactor= 1-(H - x/n(H/z_o ))/3/z

Remember this is though a approximation and might only work for low speed losses. The factor 3 (SFmultiplier) might be higher/lower.
Reamrk: More analysis of Beljaars tables, Nägeli and CFD would be needed.

Validity of the DHM formula

x/H(min) (due to non-linar behaviour of z/H and x/H) is one of the conditions for the validity of the DHM formula (see formula in above table [forth column]), the other condition is that x > 15H (being beyond the cavity boundary)

Validation of DHM formula with CFD

A validation is underway, but first a comparision between Beljaars and CFD.

Conclusions

The larger z_0m, the lower the speed factor or the smaller x; the larger the absolute difference between DHM and Beljaars becomes. Basing the formula more on the graphs of Beljaars (as also mentioned in [Werkrgoep Molenbiotoop, 1982, page 24-25]) makes it an iterative process, which might not be very practical for use. Luckily in a computer function (Excel/VBA) this is not a real problem.
IMHO the DHM formula inherits the porosity of Nägeli/Beljaars.

References

Beljaars, A.C.M.: Windbelemmering rond windmolens. In: (1979).
Judd, M.J. et al.: A wind tunnel study of turbulent flow around single and multiple windbreaks, part I: Velocity fields. In: Boundary-Layer Meteorology 80 (1996), pp. 127-165. Nägeli, Werner Weitere Untersuchungen über die Windverhältnisse im Bereich von Windschutzstreifen. In. H. Burger (ed): Mitteilungen der Schweizerischen Anstalt für das Forstliche Versuchswesen. 1946. pp. 659-737.
Townsend, A.A., The response of a turbulent boundary layer to abrupt changes in surface conditions, J. Fluid Mech, 22, 199, 1965.
Werkgroep Molenbiotoop: De inrichting van de omgeving van molens. (1982).

Acknowledgements

I would like to thank people, such as Rien Eykelenboom, and others for their help, encouragement and/or constructive feedback. Any remaining errors in methodology or results are my responsibility of course!!! If you want to provide constructive feedback, please let me know.

Disclaimer and Copyright

Home

Mail

Major content related changes: May 20, 2024