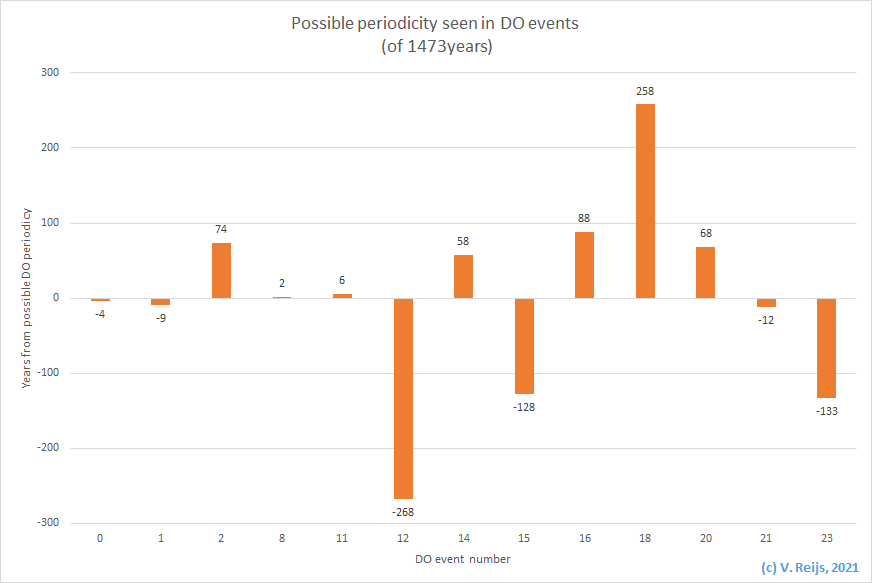Mail
NEW

Determining mean Length of Day and DeltaT formula

Using observed data for 500 BCE to 1600 CE from [Morrison&Stephenson, 2004] and for 1650 CE to 1990 CE from IERS, in the below section the change in LOD and Delta T are described.

Content

Mean Length of Day (LOD)
Linking the seen periodicity with possible geophysical events
Mean Delta T
The DeltaT formula
Can eclipses provide a clue around ndot_real?
New publication by Stephenson, et al.
References
Conclusion

Mean Length of Day (LOD)

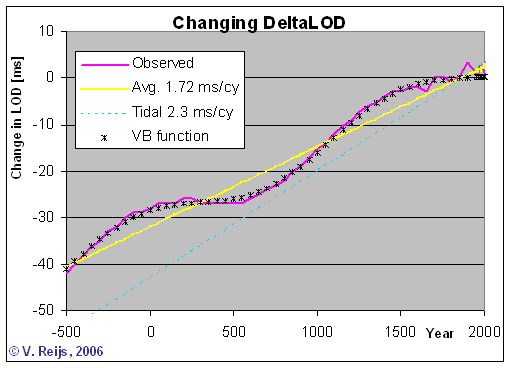
The following mean changes in Length of Day (LOD) are depicted in the below figure:

Observed mean changes [Morrison&Stephenson, 2004] in LOD (pink wavy line) (from 1650 CE is are quite accurate values)
Tidal friction influence (straight light blue dotted line) of 2.3 [ms/cy] [Stephenson, 1997, page 513]
Optimized mean changes in LOD (black crosses), this is as per my optimized function (using Simplex method with one linear and one periodic term).
The mean Solar Day function is also incorporated in the Excel XLA file for archaeoastronomy and geodesy functions.
Average mean changes in LOD (yellow straight line), is around 1.72 [ms/cy], using my own Simplex optimized function. This is within the value range (1.70+/-0.05 [ms/cy]) as provided in Stephenson ([1997], page 514)

Interesting to see that there looks to be a periodicity of around 1440 and 1550 years (also mentioned by Stephenson ([1997], page 516), if people know such a cycle and have some proof due to an astronomical/geophysical process, let me know.
It could be this periodicity is caused by the splining methodology used (based on the ideas of Slutzky [1937]), but I doubt that.
Another reason for a spurious periodicity could be due to the sampling of only a limited amount of eclipses (Stephenson's pool of observations), but I think that that would not results in such a long term periodicity, because:

I am thinking that the Nyquist-Shannon theory of sampling and low pass (anti-aliasing) filtering could be related to this idea. If this low pass filtering does not happen at half the Nyquist sampling frequency one could get spurious frequencies (f_sample +/- f_actual) in the relating analysis.
Assuming say an on average sampling of every 6 years an eclipse (pool of 400 observations over a period of 2300 years).
to get a spurious periodicity of 1550 years in an analysis, an actual periodicity of some 5.98 or 6.02 years (1/1550 = 1/6 +/- 1/actual) must exist in the real LOD (which is not 'filtered out'). Such a natural(/actual) periodicity is not likely, IMHO.
furthermore the splining in 5 knots would also not stimulate such a long term periodicity over all knot intervals (the spurious periodicity would even vary much more per knot interval; because the amount of observations varies greatly per knot interval).
In the above I used a uniform distribution of the observation, while in actual live it are random observations, but still the large variation of observation per knot interval would not give such a visible uniform long term periodicity over all knot intervals.
A test, if this periodicity is spurious, is by deliberately changing the number of observations (larger spacing between observations) and see if the periodicity changes in duration. If it is spurious, the periodicity must change according to the (1/spurious = 1/sample +/- 1/actual) formula.

Linking the seen periodicity with possible geophysical or celestial events

Stephenson [Stephenson, 1997, page 513] gives an possible explanation what causes the periodicity:

With regard to the quasi-periodic fluctuations on a timescale of some 1500 years, a possible mechanism would appear to be electromagnetic coupling between the core and the mantle of the Earth. This is the most likely cause of the decade fluctuations (Lambeck, 1980, p. 247).

A possible other reason might be the Dansgaard-Oeschger (DO) warming events (with a possible solar origin), which are events spaced by 1473 years, see also Bond [1997] (which is close to my determined periodicity value of 1440 and 1550 years). These events can be seen in Greenland ice cores and relate to glacial periods. And I think that such climate events can impact the amount of ice and thus the momentum of the Earth; thus possibly its rotation. Some researcher also see the 1470 as a superimposition of the 210 and 87 year cycles that can be recognised in respectively the DeVries-Suess and Gleissberg solar cycles [Braun, et al, 2006]. Is it important to note that the DO events seem not to have an effect on the climate in the holocene (aka present past), but the 'clock' behind DO events still exists (Rahmstorf, Pers. comm. 2016).

The astronomical year of a DO warming event is on -9655 - 1473*event#
With: event# = an positive/negative integer
The periodicity of DeltaT seems to reach zero around 1820 CE, so that a DO warming event# would be between -7 or -8 (-7.8 to be specific).

Another possible reason given by Lamb is the change of sea-level variations (Lamb, 1982); "as significant long-term alterations in climate have been detected in the last few milennia". In earlier publications Lamb (1972, pp 220) is more specific: quoting Stacey (and Pettersson) about maximum tide-generating forces happening with an approximate period of 1670 years due to a perihelion-node-apside cycle [Pettersson, 1914, pp2].
This can be checked using the FDM method, described here, looking at Anomalistic Year (related to Earth's perihelion), Draconic Month (related to Lunar nodal cycle) and Anomalistic Month (related to Lunar apse cycle). This gives a beat period of around 1250 Years (for epochs: around 1000 to 2000). So this is a different periodicity than mentioned by Pettersson.
Is this perihelion-node-apside cycle another reason for the possible periodicy in DeltaT?

So there are some different periods mentioned: DO events; 1473Years or perihelion-node-apside cycle; 1670Years [Pettersson/Stacey] and 1250Years [Reijs].

Mean Delta T

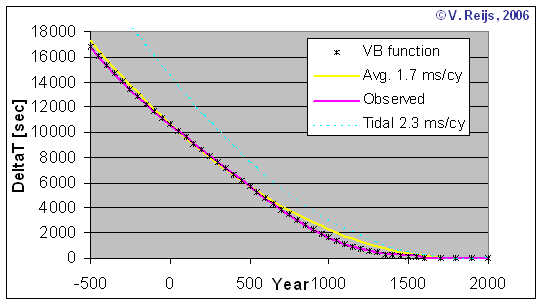
The below mean DeltaT graph is determined using the my above change in LOD formula. The following graphs are depicted:

Observed mean DeltaT [Morrison&Stephenson, 2004] (pink line)
DeltaT due to tidal friction influence (straight light blue dotted line) [Stephenson, 1997, page 513]
Optimized mean DeltaT (black crosses), this is as per the integral of my change in LOD function
This mean DeltaT function is also incorporated in the Excel XLA file for archaeoastronomy and geodesy functions.
The average mean DeltaT (yellow line) based on LOD change of around 1.7 [ms/cy] is also depicted

The DeltaT formula

Using Stephenson&Morrison [2004] as the basis (n.dot = -26"/cy^2):
StartYear = 1820 [year]
Average = 1.80 [msec/cy]
Periodicity = 1443 [year]
Amplitude = 3.76 [msec]
Y2D = 365.25
OffSetYear = (JDutfromDate(StartYear, 0) - JDNDays) / 365.25
DeltaT_VR = (OffSetYear ^ 2 / 100 / 2 * Average + Periodicity / 2 / Pi * Amplitude * (Cos((2 * Pi * OffSetYear / Periodicity)) - 1)) * Y2D [msec]

Can eclipses provide a clue around ndot_real?

Solar/lunar eclipses can not provide the real-life value of the lunar accleration (ndot_real). The argumentation is as follows:

An ephemeris is made using a certain physical model and that physical model will result in the (likely) locations of celestial bodies.
One has to start with a reasoanble accurate physical mode. Furthermore ephemerii will evolve over time (an iterative process).
From that physical model one can determine if a celestial object has an accelaration over a long period. In that way one can determine e.g. the ndot_eph (secular accelaration) of the Moon for that particular physical model/ephemeris.
So an ephemeris has such secular acceleration parameter (most of the time implicitly) included.
Using any ephemeris with a certain ndot_eph, one can calculate when the eclipse happens by varying the DeltaT (only valid for that for that ephemeris). This will give a time interval when it can be witnessed (this has been redone by the author for some 80% of Stephensons' documented eclipses (Stephenson, 1997)).
The DeltaT value/formula always needs to be accompanied by an ndot_ref value. Without such an ndot_ref value a DeltaT formula is worthless.
Remember the ndot_ref belonging to DeltaT formula is just a reference parameter, nothing more. One can always convert a DeltaT formula to another ndot_convert (Morrison&Stephenson, 2012; updated formula from McCarthy&Babcock, 1986):
ΔT_convert= ΔT_ref - 0.910747 * (ndot_convert- ndot_ref) * t² where: t = (decimalisedyear-1955.5)/100
If the ndot in real life or in an ephemeris is different than ndot_ref, one would still have an eclipse when one converts the DeltaT values to this different (possible real-life) ndot.
DeltatT formula evolves over time (due to finding more eclipse events e.g. (Stephenson, 1997) and (Huber, 2004); and/or finding a more accurate physical model behind DeltaT).
For eclipse determination: it is not important to know the ndot_real, as long as one converts the DeltaT value to the ephemeris' ndot.
It is essential to realise that the above methodology does not provide the ndot_real, the above methodology only provides an ndot based on a physical model and a DeltaT based on a specific ndot.
The ndot_real is only reductable from a theory (like within the underlaying ephemeris model) and/or matching on recorded observations.
I doubt if eclipse events can be the tool to determine the ndot_real (as one can match an eclipse with many combinations of physicalmodel/ephemeris/ndot and DeltaT formula).

IMHO, the physical models we have are not yet good enough to describe the reality around the ndot. I am not able to judge if the lunar secular acceleration (ndot_real) is definitely as determined by LLR/etc: -25.858 "/cy² (Chapront et al., 2002) or the lunar sidereal secular acceleration is -30.128 "/cy² (Henriksson, 2017). I hope astrophysic's experts can help, let me know.

New publication by Stephenson, et al.

Comparing the above derived parameters with the published values by Stephenson [2016, formula 5.1]:

Parameter	DeltaT_VR [Reijs, 2006]	Stephenson [2016]
StartYear [CE]	1820	1825
Average LOD growth [msec/cy]	1.80	1.78
Periodicity [Year]	1443	1500
Amplitude [msec]	3.76	4.0

References

Bond, Gerard, Showers William, Chesby Maziet, Lotti Rusty, Almasi Peter, deMenocal Peter, Priore Paul, Cullen Heidi, Hajdas Irka, and Bonani Georges, 'A pervasive millennial-scale cycle in North Atlantic holocene and glacial climates', Science 278, no. 5341 (1997): 1257. http://ruby.fgcu.edu/courses/twimberley/EnviroPhilo/BondPap.pdf
Braun, Holger, Marcus Christl, and Stefan Rahmstorf. 2005. 'Possible solar origin of the 1,470-glacial climate cycle demonstrated in a coupled model', Nature, Vol 438: pp. 208-11.
Chapront, J. et al.: A new determination of lunar orbital parameters, precession constant and tidal acceleration from LLR measurements. In: Astron. Astrophys 387 (2002), pp. 700-709.
Henriksson, Göran The acceleration of the Moon and the universe: The mass of the graviton. In: Advances in Astrophysics 2 (2017), issue 3, pp. 184-196. http://www.isaacpub.org/images/PaperPDF/AdAp_100064_2017041816162617572.pdf
Huber, Peter J. and Salvo de Meis: Babylonian eclipse observations from 750 BC to 1 BC. Trans. by, Mimesis 2004.
Lamb, H.H. 1972. Climate: Present, past and future (London: Methuen & Co).
McCarthy, Dennis D. and Alice K. Babcock: The length of day since 1656. In: Physics of the Earth and Planetary Interiors, 44 (1986), pp. 281-292.
Morrison, L.V. and R.W. Stephens: Observations of secular and decade changes in the Earth's rotation. In. Anny Cazenave (ed): Earth rotation: Solved and unsolved problems. Springer Netherlands 2012. pp. 69-78.
Morrison, L.V., and F. Richard Stephenson. 2004. 'Historical values of the Earth's clock error Delta T and the calculation of eclipses', Journal for the History of Astronomy, Vol 35: pp. 327-36.
Nautical Almanac Office: The Astronomical Almanac for the year 2014: And Its companion the Astronomical Almanac Online. Trans. by, U.S. Government Printing Office 2013.
Pettersson, O. 1914. "Climatic variations in historic and prehistoric time." in Svenska Hydrografik-Biologiska Kommissions Skrfiter, Vol 5. Göteborg.
Rahmstorf, Stefan. 2003. 'Timing of abrupt climate change: A precise clock', Geophysical research letters, Vol 30: pp. 17-1, 17-4.
Reijs, Victor M. M. 2006. 'Determining mean Length of Day and DeltaT formula', in http://www.archaeocosmology.org/eng/DeltaTeval.htm [accessed 30 May 2006].
Slutzky, Eugen. 1937. 'The summation of random causes as the source of cyclic processes ', Econometrica, Vol 5: pp. 105-46.
Stephenson, F. Richard. 1997. Historical eclipses and Earth's rotation (Cambridge University Press).
Stephenson, F. Richard., Leslie V. Morrison, and Catherine Y. Hohenkerk. 2016. "Measurement of the Earth's rotation: 720 BC to AD 2015." in Proceedings of the Royal society, Vol 472. in http://rspa.royalsocietypublishing.org/content/472/2196/20160404.

Conclusion

The parabolic formula provided by Stephenson to calculate the mean DeltaT is perhaps lacking enough elements to predict the DeltatT (or LOD) accurate enough over the whole time period of 500 BCE to say 1300 CE (differences smaller than 10%). This additional periodic term in the formula gives a better mapping to the table of Morrison&Stephenson than only a parabolic formula.
The periodic formula published [Stephenson, 2016] compares very well with the earlier derived formula [Reijs, 2006]: there is not that much difference in these parameter values. Reijs gives a possible reason for this periodicity: Dansgaard-Oeschger (DO) warming events.
The periodic formula has also been implemented in Stellarium since 2013. If you want to test the formula (one can use Excel XLA file), let me know.

Disclaimer and Copyright

Home

Mail

Major content related changes: May 3, 2006