NEW

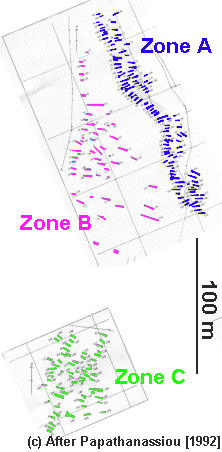

| Middle of Zone |
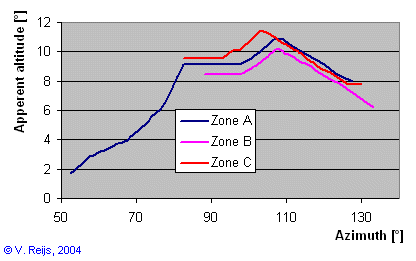
Apparent altitude |
Azimuth mountain top |
| A |
10.9° | 106° |
| B |
10.2° | 106° |
| C |
11.5° | 102° |

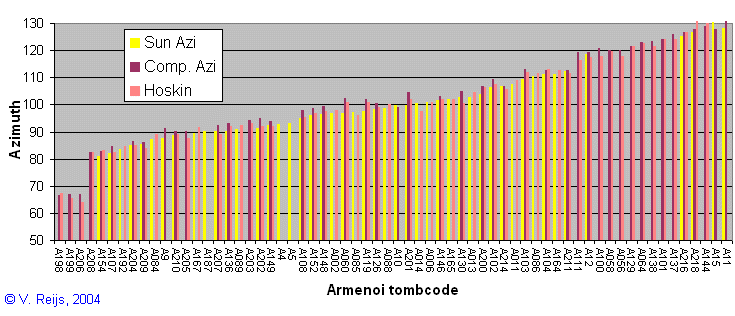
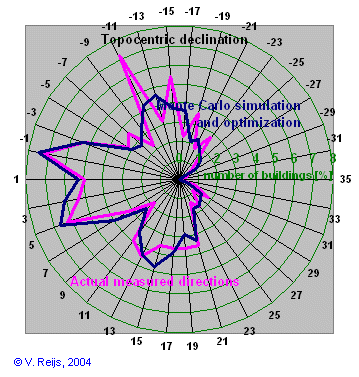
The above mentioned articles don't provide a detailed evaluation of what is visible in this distribution (except the general comment that the buildings were build in the general direction of sun/moon rise and/or aligned to a culturally lunar related Mount Vrysinas). It is of course not easy to know what was meant some 3000 years ago, but the observed distribution could perhaps provide more info. Using Monte Carlo optimization a further study has been done.
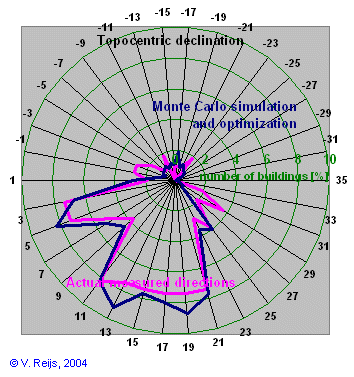 Zone A |
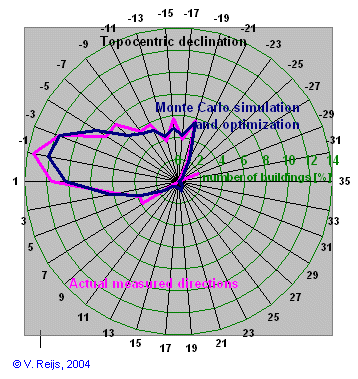 Zone B |
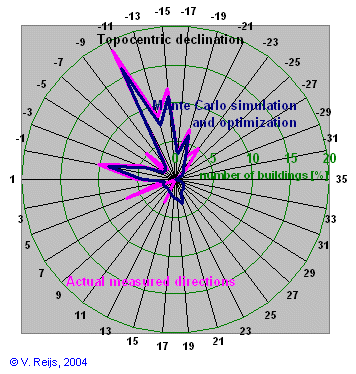 Zone C |
|
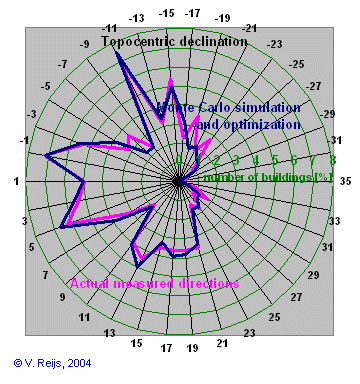 Zone ABCx |
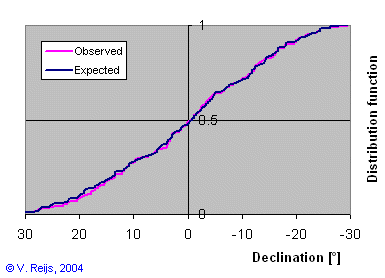 Comparing the Zone ABCx distribution functions of expected and observed. |
| Cluster of
dates (between brackets the sigma) making the following
peaks [Days] |
||||||||
| Zone/number of graves | peak4 |
peak3 |
peak2 |
peak1 |
peakA |
peakB |
peakC |
peakD |
| A/109 |
11(13) |
43(9) |
61(6) |
81(5) |
NC |
NC |
NC |
NC |
| B/52 |
NC |
NC |
NC |
NC |
95(9) |
120(19) |
NC |
149(3) |
| C/59 |
NC |
NC |
NC |
NC |
95(3) |
122(1) |
131(2) |
150(3) |
| ABCx/224 |
NC |
NC NC |
61(4) 64(9) |
82(4) 87(1) |
96(5) 98(2) |
121(1) 122(10) |
132(2) NC |
NC |
The above looks of course nice, but does this have
any linkage to cultural or archaeological findings?
So I am looking for references to important
festivals/myths/rituals/etc. occurring in the Minoan/Mycenaean
culture and Crete region around 1320 BCE (using present day
Gregorian calendar system):
| MFIRST | ELAST | EFIRST | MLAST | MHIGH | EHIGH | |
| Pleiades | May 18rd | March 23th | ||||
| Betelgeuse | July 7th | |||||
| Sirius | July 20th | Sep. 12th | ||||
| Arcturus | Sept. 4th | Feb. 18th | ||||
| Orion's belt | Nov. 1st | Sept. 4th | ||||
| Spica |
Oct. 2nd |