Determining the sensitivity for some simulated heliacal events
In the past (2006) a sensitivity
analysis was done by looking at the changing dates of the
star phases, on this web page the sensitivity of the geocentric
angles* of the involved objects will be
investigated.
In the web page two heliacal events (Morning First [MF] and
Evening Last [EL]) will be simulated by using
software. The sensitivity due to varying some12 different
parameters will be shown. Furthermore a comparison will be made
with Schoch's Arcus Visionis formula for stars [1924],
Inklaar and updated by de Jong multi-parameter criterion [Inklaar,
1989 and de Jong, 2012] and Kolev's extensive database of
observations (Kolev, 2013). It shows that Schaefer criterion's
implementation, Schoch's formula, de Jong criterion and Kolev's
observations map well. This again
supports the other earlier
benchmarking done with Schaefer's criterion.
Of course simple formula don't always provide the
most accurate results, Kolev's virtual heliacal table
(Kolev, 2013) provides a good criterion, which is also based on 3
parameters. It seems that Schaefer's or Inklaar's/de Jong's
criterion have a better handle on the complex environment. But the
large uncertainty is the atmospheric condition, which are very
difficult to post- or predict!
The benchmarking shows that a theoretical model (with no changing
of fundamental theory, only explicit parameter) can
predicts/postdict celestial visibility. There is a lot of circular
proofing going around to e.g. proof that Schoch or another simple
criterion are (in)correct, without referring to an 'independent'
theoretical model. It is important that a theoretical method is
available/possible as all other conventional one or two parameter
criterions are are only based on limited observation, so the
theoretical model can provide easy insight in many other interesting aspects around celestial
viability.
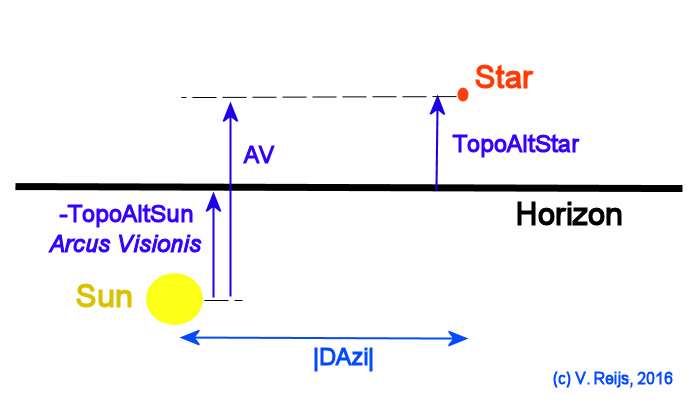
*In the below graphs the geocentric altitude
is presented, which is very close to topocentric altitudes for
star and Sun. The AV in this web site is defined as Object's
geocentric altitude minus Sun's geocentric altitude. And Arcus
Visionis is strictly defined as the Sun's geocentric
depression (which is minus the Sun's altitude).
Table of Content
Introduction
Schaefer's criterion to determine the viability of celestial objects
is not accepted by all experts. One of the main reasons might be
that most people only read the first articles on Schaefer's
criterion [1993], which has major issues. Also his software in Sky
& Telescope [1998] had some errors
(only one typo had influence on heliacal events). Luckily most inconsistencies/errors were
rectified in his 2000 article. But a lot of people based their
experience, articles and software still on these first articles,
even many years after Schaefer's published corrections (no need to
name and shame them here;-). This shows that proper literature
research, including the Internet, is essential!
Unluckily this all looks to have spread reduced confidence in
Schaefer's criterion.
Anyway Schaefer's model can solve many other
problems, such as:
- AV, Sun's (Arcus Visionis) and
object's event altitudes,
- celestial configuration differences
between the events
- Ideal First Appearance,
- daytime observations,
- analysis of
meteorological influences,
- form of visibility curve,
- variability of dates
due to several parameters,
- shadow casting,
- changing periodicity of the
MF phase,
- explain effects of photopic and scotopic
vision,
- heliacal
event depending on geography and weather conditions and
- post/prediction dates.
Luckily benchmarking the Open-source
ARCHAEOCOSMO 2002 implementation does show that Schaefer's criterion is close to
observations; the model gives a good indication of the trends
around heliacal events and many other celestial events.
Of course heliacal events are by definition difficult to pro- and
predict due to the atmospheric uncertainties, but Schaefer's model
will at least provide the tends of these influences. The
sensitivity analysis is thus also about showing these trends
beside the actual values calculated.
Software
To do this sensitivity analysis on several heliacal events, the Schaefer criterion has been used. The
implementation of that criterion is part of the Open-source
packages: ARCHAEOCOSMO Excel
plug-in and Swiss
Ephemeris. Both use DE405 and
Morrison&Stephenson&Hohenkerk [2016] for DeltaT.
Variation of parameters
For the sensitivity analysis I used a fictive star that is close
to Alcyone, with using a default Declination of +24.1°, RA
of 3h47m and Magnitude of 3 (instead of Alcyone's Declination is
+24.1°, RA is 3h47m and Magnitude is 2.87). The
observations have been simulated around 50CE for a German
location. Furthermore using standard
atmosphere (15 °C and 1013.25 mbar) with a relative
humidity of 30%. The age of the observer is taken as 30 years with
the average acuity of ~1.4 [snellen].
The Default values used for these parameters are shown in below
table, beside the used Minimum and Maximum (and the results) or
this sensitivity analysis:
Parameter
|
Astr.
Year |
Longitude
[°]
|
Latitude
[°]
|
Height
[m]
|
Temperature
[°C]
|
Air
Pressure
[mbar]
|
Relative
Humidity
[%]
|
Astr. Ext.
Coeff.
**
|
Acuity
[snellen]+
|
Age |
Star's
Declination [°]+ |
Stars' Right Ascension [h]
|
Star's
Magnitude+
|
Minimum
|
-50
|
0 |
30 |
150
|
0 |
913.25 |
0 |
0.15 |
0.7
|
20 |
-30.1
|
-4.73
|
-4
|
Default
|
50
|
7.5
|
47.5
|
350
|
15
|
1013.25
|
30
|
0.32
|
1.4
|
30
|
24.1
|
3.27
|
3
|
Maximum
|
150 |
15 |
65 |
550 |
30 |
1113.25 |
60 |
0.49 |
2.8
|
40
|
30.1
|
11.27
|
4
|
Resulting sensitivity
in star's MF altitude
|
3%
|
2%
|
48%
|
8%
|
15%
|
15%
|
30%
|
69%
|
47%
|
8%
|
20%
|
5%* |
73%
|
Resulting sensitivity in
star's MF date [days]***
|
+1
|
+1
|
+51
|
-1
|
+2
|
+3
|
+4
|
+11
|
-21
|
+2
|
-49
|
178
|
37
|
Resulting sensitivity
in star's EL altitude |
low*
|
0%
|
low* |
low* |
low* |
low* |
low* |
42%
|
66%
|
low* |
low*
|
low* |
58%
|
Resulting sensitivity in star's EL date
[days]***
|
+2
|
0
|
-5
|
0
|
-1
|
-1
|
-2
|
-9
|
+12
|
0
|
36
|
78
|
-11
|
* Due to the effect of changing between scotopic and photopic
vision, there is some 35% resulting sensitivity, but overall no
significant systematic increase/decrease is seen.
** When varying the atmospheric parameters Temperature, Air Pressure
and Relative Humidity; the Atmospheric Extinction Coefficient is
fully determined by these atmospheric parameters.
***Resulting variation in days due the Minimum and Maximum value of
parameters (compared to Default)
+These parameters have a Default that is different than the average
of Minimum and Maximum.
Sensitivity
The sensitivity analysis has been done for two star phases:
Morning First (MF) phase
For the sensitivity analysis, the star's morning first (MF)
observations have been simulated.
Below are graphs of star's geocentric event altitude and the Sun's
geocentric event altitude at the star's MF phase. Each shows the
influence due to changing one parameter between its Minimum and
Maximum value (x-axis), while keeping the other parameters on their
Default values.
Parameters that don't have much influence
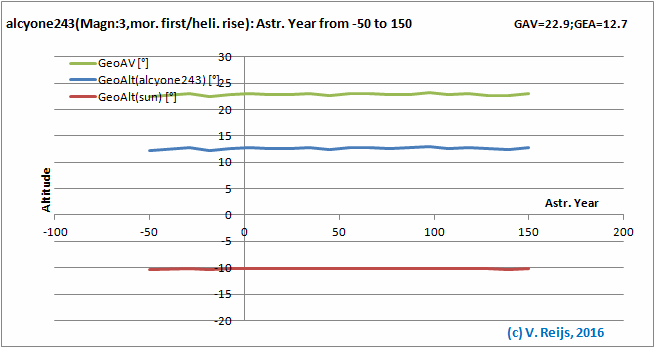 Astronomical Year: almost no influence
Astronomical Year: almost no influence
 Longitude: almost no influence
Longitude: almost no influence
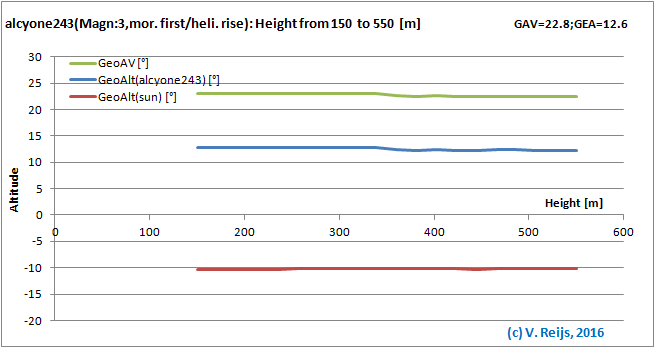 Observer Height: almost no influence.
Observer Height: almost no influence.
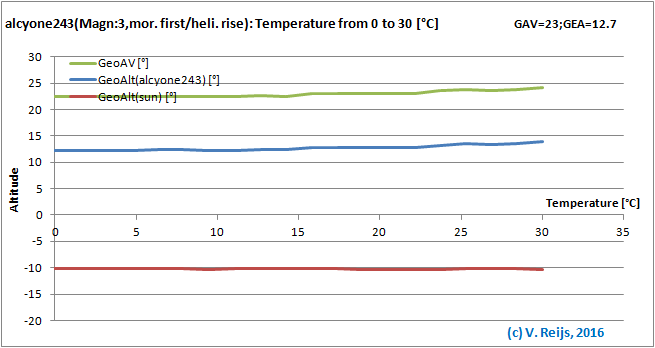 Temperature: almost no influence.
Temperature: almost no influence.
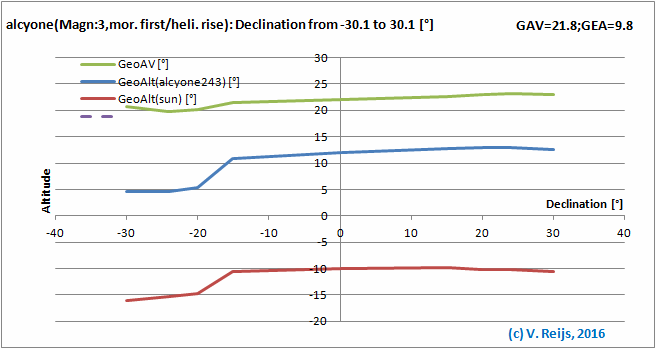 Star's Declination: almost no influence (except the
discontinuity from night [scotopic] to day [photopic] vision).
Star's Declination: almost no influence (except the
discontinuity from night [scotopic] to day [photopic] vision).
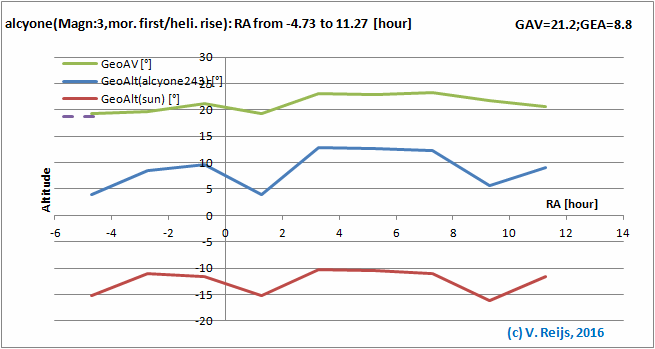 Star's Right Ascension: some influence
(mainly due to discontinuity from night [scotopic] to day
[photopic] vision).
Star's Right Ascension: some influence
(mainly due to discontinuity from night [scotopic] to day
[photopic] vision).
Parameters that have influence on two altitudes
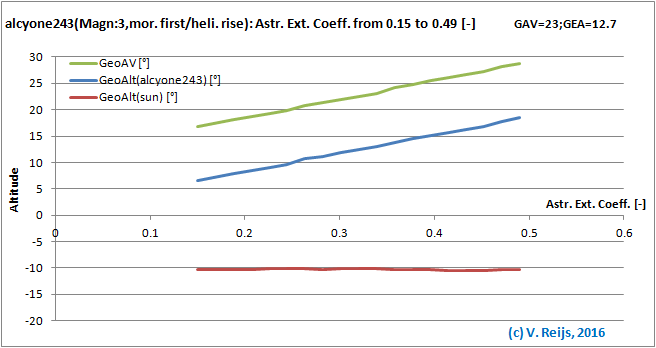
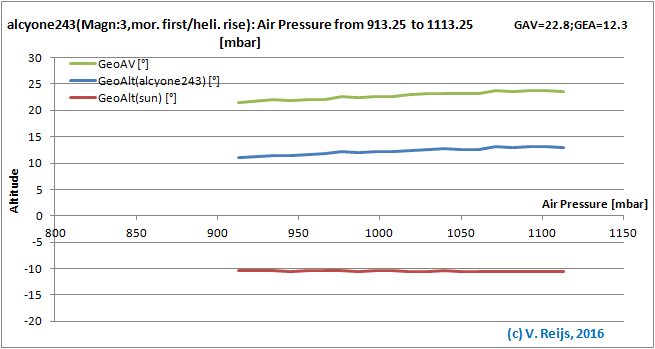 Air pressure: the higher the Air Pressure the higher
the AV and star's event altitude.
Air pressure: the higher the Air Pressure the higher
the AV and star's event altitude.
The Sun's event altitude stays almost the same.
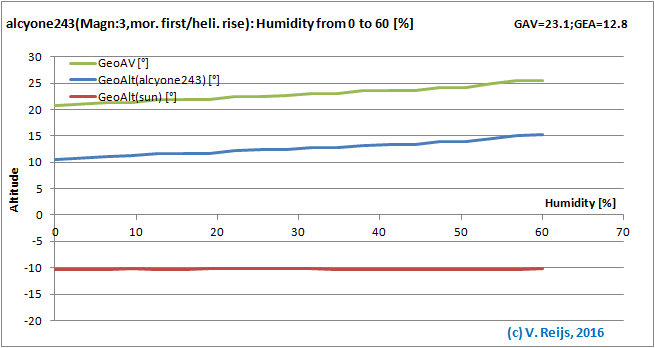 Relative humidity: the higher the Relative Humidity the higher
the AV and star's event altitude.
The Sun's event altitude stays almost the same.
Relative humidity: the higher the Relative Humidity the higher
the AV and star's event altitude.
The Sun's event altitude stays almost the same.
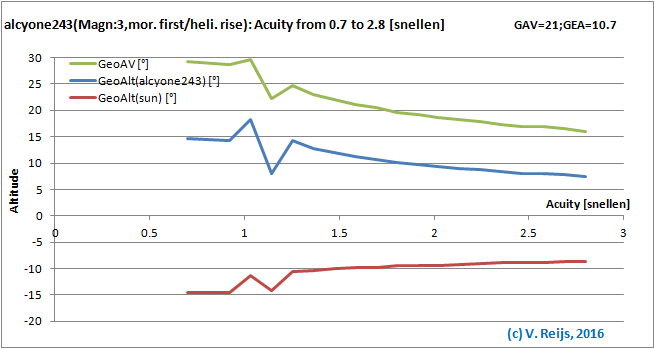 Observer Acuity: the better the observer Acuity the lower the
AV
and star's event altitude; and the higher the Sun's event
altitude.
Observer Acuity: the better the observer Acuity the lower the
AV
and star's event altitude; and the higher the Sun's event
altitude.
The discontinuity is due to change from night (scotopic)
to day (photopic) vision.
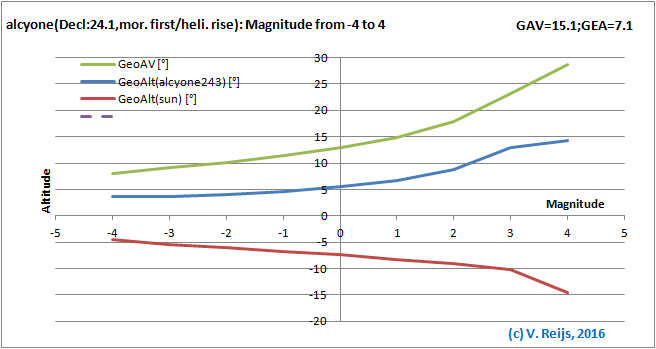 Star's Magnitude: the higher the Magnitude the higher the AV
and star's event altitude; and the lower the Sun's event
altitude.
Star's Magnitude: the higher the Magnitude the higher the AV
and star's event altitude; and the lower the Sun's event
altitude.
The discontinuity is due to change from
night (scotopic) to day (photopic) vision.
Evening Last (EL) phase
For the sensitivity analysis, the star's evening last (EL)
observations have been simulated.
Below are graphs of geocentric AV, star's geocentric event altitude
and the Sun's geocentric event altitude on the star's EL phase. Each
shows the influence due to changing one parameter between its
Minimum and Maximum value (x-axis), while keeping the other
parameters on their Default values.
Parameters that don't have much influence
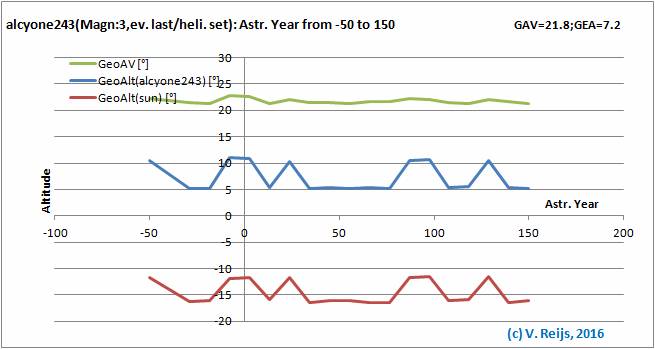 Astronomical Year: almost no influence (except the
discontinuity from night [scotopic] to day [photopic] vision).
Astronomical Year: almost no influence (except the
discontinuity from night [scotopic] to day [photopic] vision).
 Longitude: almost no influence
Longitude: almost no influence
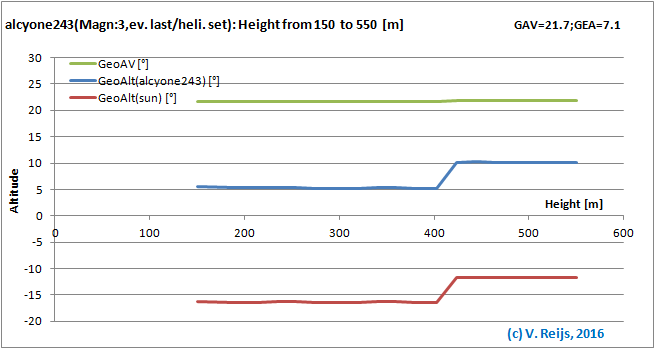 Observer Height: almost no influence (except the
discontinuity from night [scotopic] to day [photopic] vision).
Observer Height: almost no influence (except the
discontinuity from night [scotopic] to day [photopic] vision).
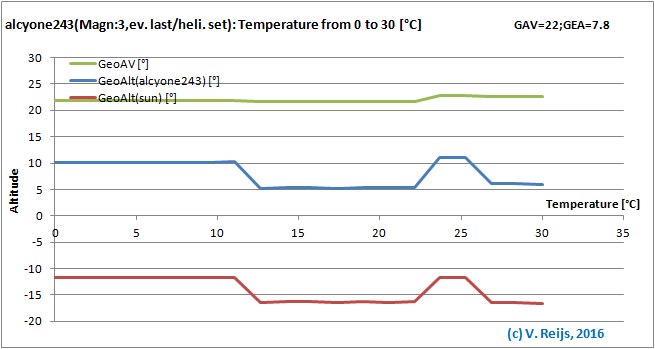 Temperature:
almost no influence (except the discontinuity from night
[scotopic] to day [photopic] vision).
Temperature:
almost no influence (except the discontinuity from night
[scotopic] to day [photopic] vision).
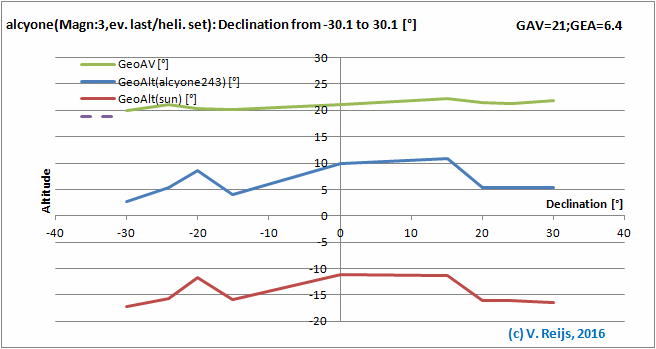 Star's Declination: almost no influence (except the
discontinuity from night [scotopic] to day [photopic] vision).
Star's Declination: almost no influence (except the
discontinuity from night [scotopic] to day [photopic] vision).
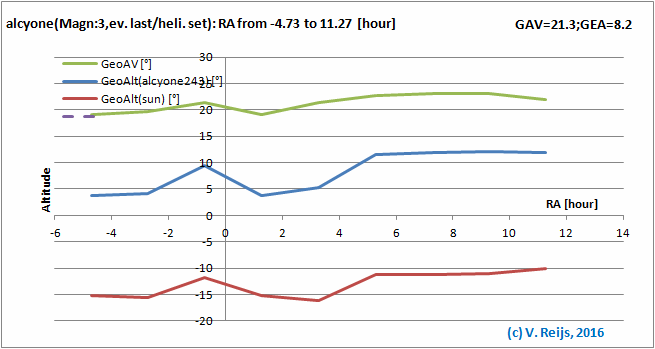
Star's Right Ascension: some influence (mainly due to
discontinuity from night [scotopic] to day [photopic]
vision).
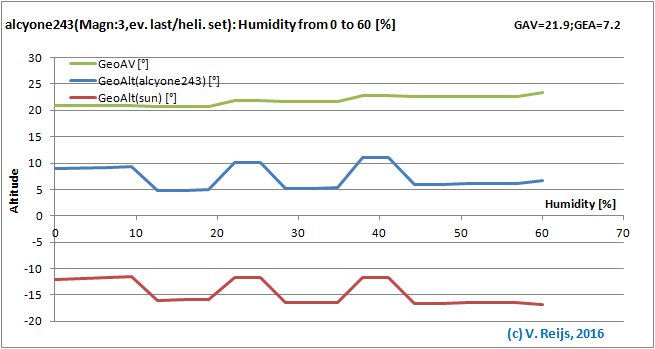 Relative humidity: almost no influence (except the
discontinuity from night [scotopic] to day [photopic] vision).
Relative humidity: almost no influence (except the
discontinuity from night [scotopic] to day [photopic] vision).
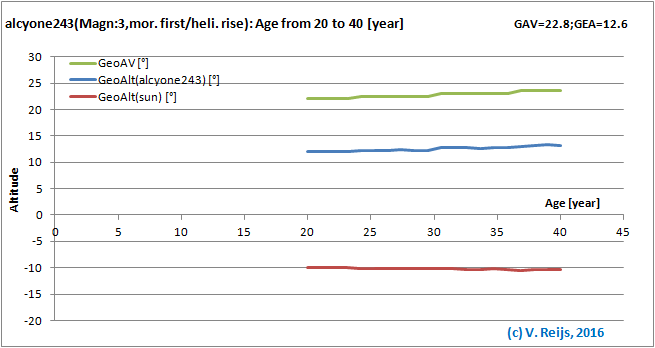
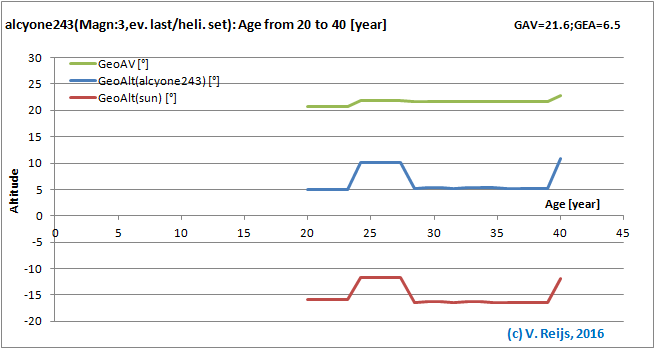 Observer Age: almost no influence (except the
discontinuity from night [scotopic] to day [photopic] vision).
Observer Age: almost no influence (except the
discontinuity from night [scotopic] to day [photopic] vision).
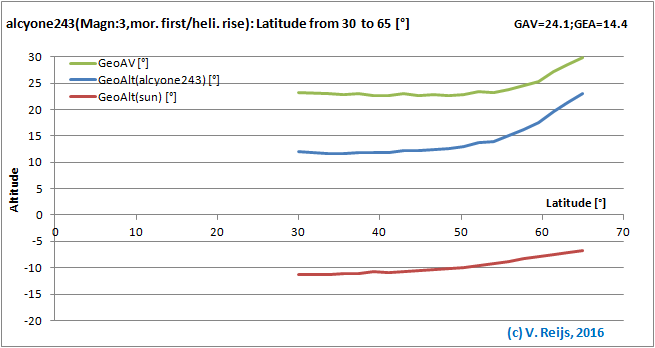
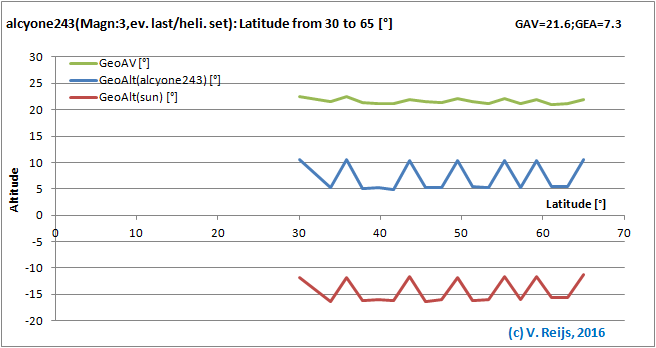 Latitude: almost no influence (except the
discontinuity from night [scotopic] to day [photopic] vision).
Latitude: almost no influence (except the
discontinuity from night [scotopic] to day [photopic] vision).
Parameters that have influence on two altitudes
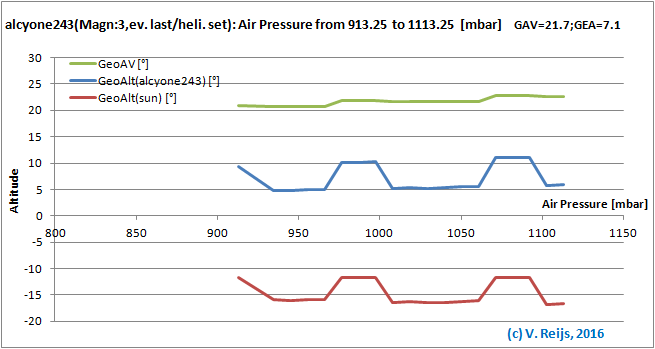 Air pressure: the higher the Air Pressure the higher
the AV and star's event altitude.
Air pressure: the higher the Air Pressure the higher
the AV and star's event altitude.
The Sun's event altitude stays almost the same.
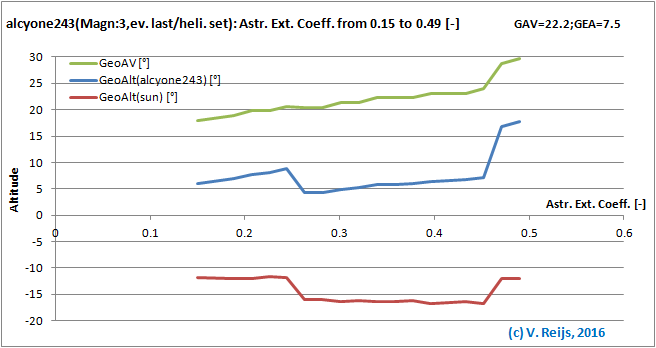 Atmospheric Extinction Coefficient: the higher the Atmospheric
Extinction Efficient
the higher the geocentric AV and star's event altitude.
The Sun's event altitude stays almost the same
Atmospheric Extinction Coefficient: the higher the Atmospheric
Extinction Efficient
the higher the geocentric AV and star's event altitude.
The Sun's event altitude stays almost the same
Parameters that have influence on three altitudes
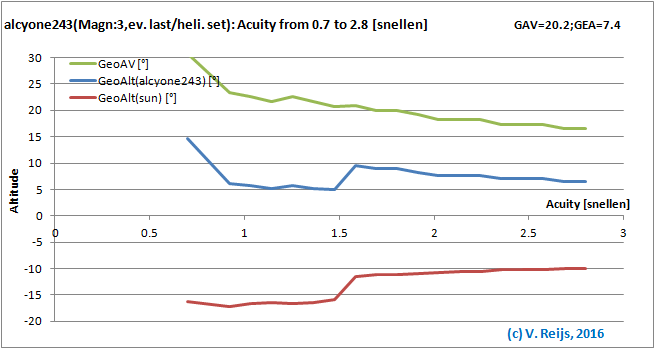 Observer Acuity: the better the observer Acuity the lower the
AV
and star's event altitude; and the higher
the Sun's event altitude.
Observer Acuity: the better the observer Acuity the lower the
AV
and star's event altitude; and the higher
the Sun's event altitude.
The discontinuity is due to change from night (scotopic)
to day (photopic) vision.
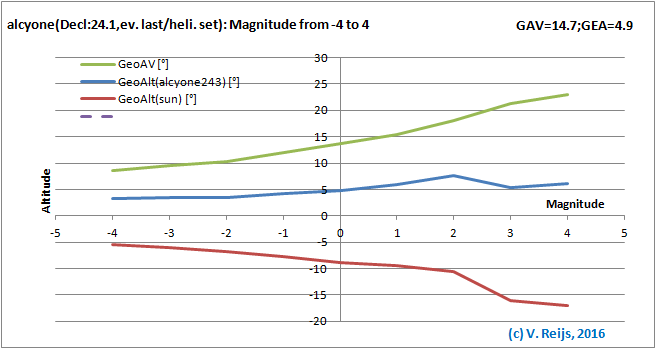 Star's Magnitude: the higher the Magnitude the higher the AV
and star's event altitude; and the lower
the Sun's event altitude.
Star's Magnitude: the higher the Magnitude the higher the AV
and star's event altitude; and the lower
the Sun's event altitude.
The discontinuity is due to change from night (scotopic)
to day (photopic) vision. Evaluation
In the above
table one can also see the sensitivity due to the resulting
variation of the specific parameter for MF and EL phases. The
yellowed cells show that the resulting sensitivity (seen in Minimum
or Maximum star's event altitudes) is more than 10% from the average
star's event altitude.
General
A few general observations:
- The variation of Acuity and Magnitude are similar (as Acuity
changes the detection of Magnitude in a linear way).
- The Sun's event altitude does not really change when other
parameters are changed. It only changes when varying: Latitude
(in case of MF), Acuity and Magnitude.
- As the Sun's event altitude at MF or EL phase is quite stable
for a certain Magnitude (and the observer's Acuity and
Latitude), one can determine from the actual object's event
altitude the atmospheric conditions.
- The Object altitude is quite linear dependent on the AEC (as
also observed by Kolev, 2013, page 243)
- The switch between scotopic (night) and photopic (day) vision
results in a discontinuity of some 5°. In real live these
discontinuities will be smoothed out, due to the slow adjustment
of the eye between these two visions.
- The dependency on the Atmospheric Extinction Coefficient,
Acuity and Magnitude is for MF and EL phases more or less
similar (in value/form).
MF phase
The parameters that have significant influence on MF phase
are: Latitude, Relative Humidity, Atmospheric Extinction
Coefficient, Acuity, Declination and Magnitude.
If the Latitude is between 30 and 54° (so between Egypt up to
middle of UK), the sensitivity is lower than 10% of the star's event
altitude.
Relative Humidity and Atmospheric Extinction Coefficient are related
with the atmospheric conditions.
EL phase
The parameters that have significant influence on EL phase
are: Atmospheric Extinction Coefficient, Acuity and Magnitude.
Atmospheric Extinction Coefficient is related with the atmospheric
conditions.
Overall
EL phase seems to be less depending on Latitude, Relative Humidity
and Declination than the MF phase. For the EL phase the influence of
scotopic and photopic visions is more pronounced than the MF phase.
Comparing Schoch and Schaefer criterions
<It looks that Schoch's arcus
visionis is in effect the AV definition>
In below graph the MF and EL phases of Schaefer's criterion (with
Latitude is 33°, Atmospheric Extinction Coefficient of 0.15
[very clear skies], star's Declination of 0.1° and RA of
3h16m [called alcyone01]) are compared with the Schoch
criterion (derived from Babylonian and Greek observations for
near ecliptic stars: [1924], page 734).
The MF phase matches with Schoch, while the EL phase somewhat less.
The differences seen by Schoch [EL<MF] and Schaefer [MF<EL]
can perhaps partly be explained that Schoch uses an averaged
criterion, while Schaefer includes the actual path difference of Sun
and star.
The general tend supports my earlier
benchmarkings.
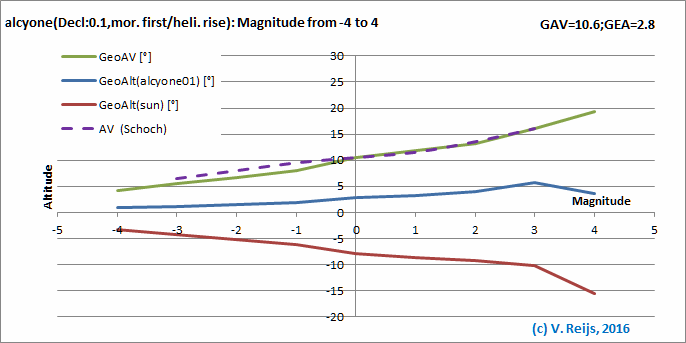 Morning First phase
Morning First phase
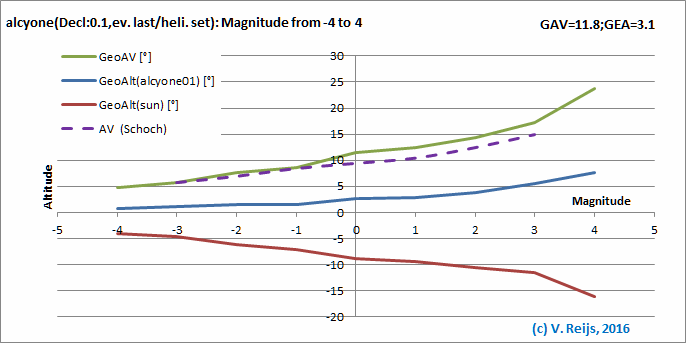 Evening Last phase
Evening Last phase
The Schaefer's AV (green line) is close to
Schoch's AV (purple dashed line)
In the above MF and EL phase graphs a difference
is seen in the star's and Sun's event altitude. The main reasons for
this are: the relative position of the star and Sun at these
different event (MF in June and EL in March) is different (e.g. a
difference in delta azimuth [DAzi] of some 35°, which gives a
difference of at least some 0.6
or more degrees); and the dependency on the Month/season.
Pachner [2010] does not recommend different criterions for EL and MF
phases.
The formula for Arcus Visionis or AV in literature only
include the Magnitude as a linear parameter (although when reading
the original reference they sometimes talk about the geographical
region). These formula also do not provide the value for the star's
or Sun's event altitude.
If we stay between Egypt and mid UK; the Latitude can be removed
from the list of important parameters, thus atmospheric conditions
(mainly Relative Humidity and the resulting Atmospheric Extinction
Coefficient), Acuity and scotopic/photopic vision have the largest
influence beside Magnitude.
The lack of these parameters make the simple formula/tables somewhat
inaccurate.
Comparing Kolev observations with Schaefer
criterion
<Kolev uses the definition of AV: difference between Object's and
Sun's topocentric altitude>
Kolev has set an excellent database with regard to heliacal event
observations (Kolev, 2013, Appendix F)!
His observations included: object, observer, AEC, location, phase,
date, first-, best-, and last observation time. I have not encounter
similar (essential) detail of heliacal event observations! Excellent
work by Kolev!
The Sun's altitude (orange dots) and star's altitude (blue squares)
of Kolev's 80 MF and 81 EL observations of stars and planets (Kolev,
2013) are provided in below graph (the [best] altitudes are the
average altitudes at the time of first and last observed during MF
or EL). The observed Sun's altitude stays, as expected, below the
theoretical line of Schaefer's Sun altitude (alcyone01 is a
fictive star at declination 0.1° and varies its magnitude from -4 to
4). The observed Stars' altitudes are, as expected, between the
Schaefer's star's altitude lines of AEC = 0.16 and 0.46; as Kolev's
observations are in that AEC range. This again supports my
earlier benchmarkings.
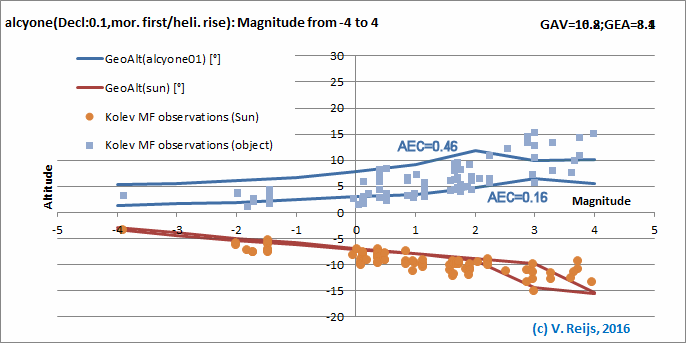 Morning First phase
Morning First phase
It looks that for MFs the spread of the
observed (Kolev) and calculated (Schaefer) object altitudes are
similar.
Important to realise that the observed best time has been chosen
as the average of first and last observation times. This is not
hundred percent accurate. Also Schaefer's lines are derived for
average circumstances and Dec/RA of alcyone01. So the
graphs presented are only illustrative.
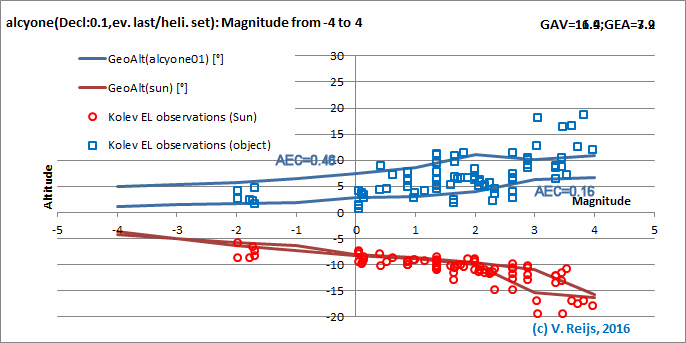 Evening Last phase
Evening Last phase
It looks that the ELs for the observed (Kolev)
altitudes have a larger spread than the calculated (Schaefer)
altitudes,
The spread of the observed object's altitudes is for EL larger
than for the MT observations.
There looks to be no real difference of the Sun's altitudes for
EL and MF observations, but for Schaefer's implementation there
is a difference.
Magnitudes above 2 to 3 are perhaps not well predicted with
Schaefer's model. this due to the change from photopic (day) to
scotopic (night) vision. This could be due the variability of
scotopic vision in the individuals (Carr&Fisher, 1970).
Interesting to see that the
Arcus Visionis (Sun's
depression) looks to be quite stable, while the Object's
altitude is varying quite a lot (depending on the AEC).
Influence of
day/night vision
Kolev also investigated the observed difference between the
Object's altitude and the AEC, by looking at:
dAlt/dAEC
(Kolev, 2013, page 260):
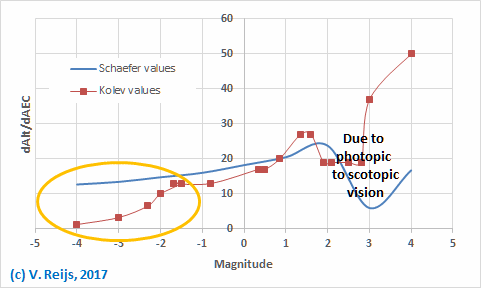
Interesting to see the dip due to change
over from photopic to scotopic vision (around Magn=1.5 for
Kolev and Magn=2 for Schaefer). The Magnitude where this
happens might indeed depend on the observer (perhaps this
should be a new parameter in Schaefer's criterion?). Kolev
does not explain this dip, but Schaefer's criterion looks to
be able to provide a reason for this dip.
The differences for low magnitudes (within the orange oval:
Magn=-4 to -1.5) could
be due to two
reasons: Kolev does not start its criterion with
AEC=0, but with AEC=0.16; and secondly he does not allow
BaseAltObj to be smaller than zero (which would be the case
for planets). Schaefer's criterion provides direction here.
Kolev
inferred his criterion (no analytic model),
as others, from observational data (Kolev, 2013, page
260-263).
More information about Kolev'
criterion can be found
here.
Comparing de Jong and Schaefer
criterions
<Inklaar, de Jong and Schaefer use the same definition of AV:
difference between Object's and Sun's topocentric altitude>
Inklaar made also a model for the visibility [Inklaar, 1989] and de
Jong used this with slight updates [de Jong, 2012] in an article
around Sirius [de Jong, 2006]. For the MF phase, location Cairo and
1000 BCE, the following results can be compared between Reijs and de
Jong [2006, Table 1]:
 Comparing the results of Reijs and de Jong for Sirius MF
Comparing the results of Reijs and de Jong for Sirius MF
<Opt. time for de Jong has been calculated:
First time+Duration/2-DeltaTDifference>
<Reijs>/<de Jong>.
There are indeed some differences in Sirius' and Sun's event
altitudes. The timing difference could be explained by two facts:
- de Jong's time is the first visibility of Sirius, while Reijs'
time is the optimum visibility time.
- each model uses a different DeltaT formula: de Jong [2012]
uses Morrison&Stephenson [1982] and Reijs uses
Morrison&Stephenson [2004]. This gives a DeltaT difference
of ~4 minutes.
The AVs are more or less the same, and also the dates for the MF
phase are the same. There is good agreement between the two
multi-parameter criterions!
Differences between Inklaar, de Jong
and Schaefer criterions
Inklaar's and Schaefer's criterions were 'born' more or less in
the same period (mid 1980s). Inklaar's model has been slightly
updated by de Jong (2012). Schaefer's last model description is
from 2000.
Functions in criterion
|
Inklaar (1998)
|
de Jong (2012)
|
Schaefer (2000) & ARCHAEOCOSMO
(Reijs, 2006)
|
Definition of AV
|
Difference Sun's altitude and star's
topocentric altitude
|
Difference Sun's altitude and star's
topocentric altitude |
Difference Sun's altitude and star's
topocentric altitude |
Atmospheric extinction coefficient
|
fixed values
|
fixed values
|
fixed value or atmospheric parameters
(Schaefer, 1993)
|
Aimass
|
reasonable accurate (Rozenberg, 1966)
|
reasonable accurate (Rozenberg, 1966) |
reasonable accurate (Rozenberg, 1966)
or accurate (Schaefer, 1989)
|
| Light loss |
reasonable accuracy
|
reasonable accuracy
|
reasonable accuracy or accurate |
| Sun's Sky brightness |
inter/extrapolation of Maryland (USA)
(Koomen, 1952) |
inter/extrapolation of Maryland (USA)
(Koomen, 1952)
|
formula (Krisciunas and Schaefer, 1991) |
Moon's Sky brightness
|
none
|
none
|
formula (Krisciunas and Schaefer, 1991) |
Point source visibility
|
(Hecht, 1947)
|
based on Tousey and Koomen (1953) (de Jong,
2012)
|
(Hecht, 1947)
|
Visibility threshold
|
50, 90, 98% (Hecht, 1947) |
50, 90, 98% (Hecht, 1947) |
50, 90, 98% (Hecht, 1947) |
Extended source visibility
|
none
|
none
|
(Blackwell, 1946)
|
DeltaT
|
none
|
(Morrison and Stephenson, 1982) |
(Morrison and Stephenson, 2004)
|
This and the above section shown there is good agreement between the
these multi-parameter criterions. Remember this does not say if the
results of these criterions are matching that they would match
observations, as these criterions use almost identical functions.
More extensive benchmarking is thus
essential.
Ptolemy's definition of Arcus Visionis
<see also some other
discussion around the definition of Arcus Visionis and AV>
Ptolemy's Arcus Visionis definition seems to be the altitude
of Sun at the MF&EL heliacal event. In the pages about
visibility of fixed stars (Toomer, page 404-416) the word '[Arcus
Visionis]' is mentioned by the translator (Toomer, page 413):
For it is not possible to find the size of the arc by
which the sun must be removed below the horizon in order for a
given star to have its first or last visibility... For that arc
[the arcus visionis] cannot be the same for all stars nor
the same for a given star at all places [on earth], but varies
according to the magnitude of the star, its distance in latitude
from the sun, and the change in the inclination of the ecliptic
[with respect to the earth]. (Toomer, page 413)
The definition Schoch uses is as follows:
The arcus visionis (in this paper called γ) of
a planet or of Sirius is the depression of the Sun below the
horizon, measured in the vertical circle for the moment when the
star sets on the last evening when it is visible or rises on the
first morning when it is visible. refraction disregarded in the
case of both bodies. (Schoch, 1924, page 731)
This could indicates that 'arcus visionis' is the Sun's
altitude, but strangely Schoch states "refraction being disregarded
in the case of both bodies" (Schoch, 1924, page 731) as there is
only one body mentioned (the Sun) and it is below the horizon so
refraction is not in play...
But comparing Schoch's
criterion with Kolev's observations, it looks that Schoch uses
AV instead of Arcus Visionis, so his comment about
refraction and variability due to atmosphere points to his use of
AV.
According to Neugebauer:
Hence Ptolemy associates with a given star and a
specific phase a characteristic parameter, the depression h
of the sun below the horizon (the "arcus visionis" in
modern terminology) at which the phenomenon takes place. In order
to find h at a given geographical latitude φo
(e.g. Alexandria) one must establish, by actual observation, the
date and hour of the phase... (Neugebauer, 1975, page 927)
Ptolemy (and Neugebauer???) defines the Sun's altitude as the Arcus
Visionis, instead of the Object's altitude minus the Sun's
altitude. More modern sources (e.g. Schoch, Schaefer, Inklaar,
de Jong and Kolev) though state that AV is the difference between
Sun's and object's topocentric altitude.
Analysing the above pictures an interesting
aspect surfaces: the Sun's altitude is constant for a specific
Magnitude when changing most the other parameters; except when
related to the visual perception: Acuity and Age.
In the Almagest (translation by Toomer, 1984, page 414-415) we read
similar:
... the [vertical] distance to the sun below the earth
is always remain equal to Zθ {Sun's altitude} for the same
star.since, for an equal interval so taken , the [effect of] the
rays above the earth will be similar... However if the arc
corresponding to the Zθ {Sun's altitude} remains constant
everywhere on earth for the same stars (as seems likely, since the
fixed stars too must be affected by the variation in the
atmosphere in the same way as the rays are), the distance observed
at a single terrestrial latitude will suffice us to determine
those at the other latitudes [we can do this] by geometrical
methods, whether the variation in the inclination of the ecliptic
is due to the terrestrial location or to the demonstrated motion
if the ps here of the fixed stars towards the rest with respect to
it [the ecliptic]. ... Once this [Sun's altitude] has been found,
and provided that it remains the same for all locations, we can
use it to derive the {ecliptic distance Sun and star} at [all]
other terrestrial latitudes from the same considerations.
[]: additions by the translator, Toomer, to explain
Greek
(): additions by the author; Ptolemy, to explain
{}; additions by Reijs; to map on modern terminology
Ptolemy states "However if the arc corresponding to the Zθ
{Sun's altitude} remains constant everywhere on earth for the same
stars (as seems likely, since the fixed stars too must be affected
by the variation in the atmosphere in the same way as the rays are)"
(Toomer, 1984, page 414). This maps quite well with what is seen in
above picture (derived from the implementation of Schaefer's
criterion).
An experiment to simulate this further is
by reducing Atmospheric Extinction Coefficient towards zero and see
if the Sun's altitude stays more or less at the same level (even
below AEC=0.15). See below picture (instead of max. accuracy formula
used in the above pictures, the reasonable accuracy formula has been
used to allow for the unrealistic AECs).
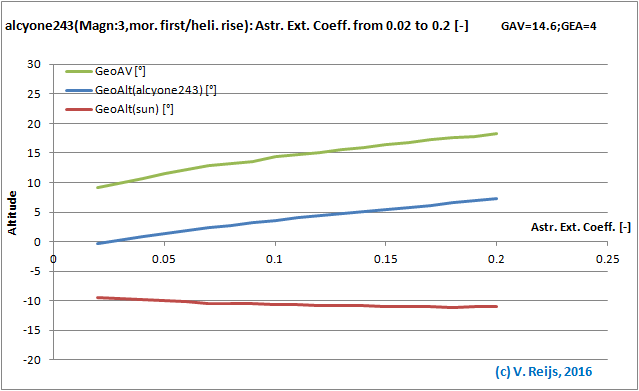 Atmospheric Extinction Coefficient: For AEC smaller than 0.15
(not realistic),
Atmospheric Extinction Coefficient: For AEC smaller than 0.15
(not realistic),
the Sun's altitude stays more or less at the same level.
So Sun's altitude stays quite constant down to very small
(unrealistic) AECs! This observation explains why Ptolemy's
definition (object on horizon: Arcus Visonis) works very
well theoretically and has practical value. So Ptolemy's theoretical
derivation maps well on an earth without refraction and extinction
(aka a topocentric definition). And this Arcus Visionis can
be easily transformed by adding a factor linearly depending on the AEC, to derive the AV.
This seems not to be well understand by reviewers of Ptolemy, etc;
see also next section.
A paradox
I realise there might be a paradox that is related to the Arcus
Visionis (depression of the Sun) and the AV (difference
between star and Sun altitude), both at the moment of MF&ML&EF&EL visibility:
- The Arcus Visionis is the depression of the Sun.
- At the true event the star is at zero topocentric altitude,
and one can easily follow the geometry description of Ptolemy
- Reading the Arcus Visionis definition of Ptolemy and
Neugebauer, they all look to be using the Sun's depression (Arcus
Visionis) for the visible/apparent rise/set event.
Neugebauer refers to Ptolemy.
- Only mentioning the depression of the Sun does not really help
(as that happens every day;-). So the notion that the star is
near the horizon during this apparent event is still important;
as the apparent event will happen a few days before/after the
true event (when the star is at zero and the Sun at Arcus
Visionis).
All the above sounds logical... But now:
- Should one wait (a few minutes) until the star is at zero
topocentric altitude on the day of the an apparent event?
At this moment the Sun's depression is close to the AV... But
this seems not to be meant when saying 'at zero topocentric
altitude'.
- It is interesting to see that the Sun's depression at the true
or apparent star's phase is almost independent of the
atmospheric condition (see above graph,
where the AEC changes from 0.02 to 0.15!!!).
- One could read a similar stability of the Arcus Visionis
in Ptolemy's reasoning (see above
quote from page 414).
At least I read that in that text... You too? Let me know.
- So Arcus Visionis is a relatively stable number (if
the observer's acuity stays the same).
- So the question is: Why does Neugebauer still say that the Arcus
Visionis is very depending on the atmosphere?
So I don't fully understand what Neugebauer (and others) are
saying... So I think the above is a proper
evaluation or do I make somewhere an error. Let me know.
According to Inklaar (1989, page 13) and Evans (1998, page 201-204)
the apparent helical events (visibility of the star) was possibly
used to predict the weather (Toomer, page 417). And of course the
star's altitude at the heliacal event is depending
on the atmospheric parameters (such as AEC). So was the star's
altitude at a heliacal event used for weather predictions?
Visibility of Alcyone during the year 50 CE
In the below graph one can see when Alcyone is visible (green), when
its Magnitude is below extinction (red) or when it is below the
horizon (yellow). The white curve is Sun rise. The repeating red
boxes (invisibility) near Alcyone's set and rise are due to Moon
light.
The horizontal axis are days in 50CE (left top = Jan 1) and vertical
axis is 24 hours (left bottom = 00:00 GMT). Using Default setting
from above table.
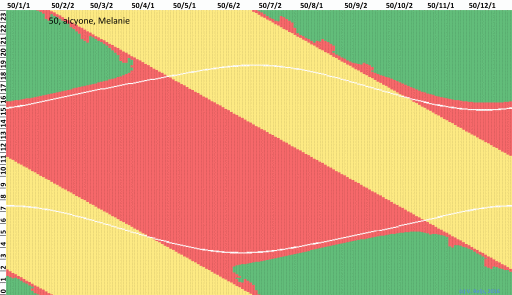 Alcyone with influence of Moon light (using Schaefer)
Alcyone with influence of Moon light (using Schaefer)
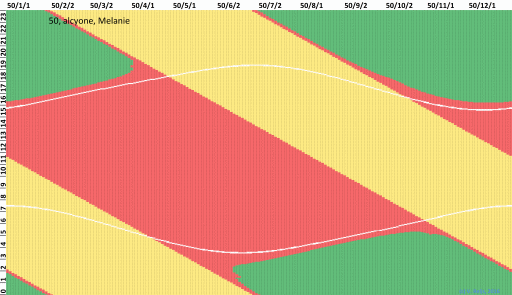 Alcyone without influence of Moon light (using Schaefer)
Alcyone without influence of Moon light (using Schaefer)
Similar graphs can be gotten using the software
Planetary,
Stellar and Lunar Visibility. The difference is that PSLV
only uses a two parameter criterion. See the somewhat adjusted
(differently colored) screen grab from PSLV: dates marked are
determined by
PSLV/Schoch's
criterion, which map very well on Schaefer's results:
 Alcyone without influence of Moon light (using PLSV)
Alcyone without influence of Moon light (using PLSV)
Visibility of Venus during
the year 50 CE
The visibility of Venus can be see below. As one can see,
Venus is visible not only when the Sun is below the
horizon, but also during the day at some moments of the
year. A day-time observation by Curtis in literature is
also analysed here.
PLSV is not able to produce graphs that include daytime
visibility of the celestial object.
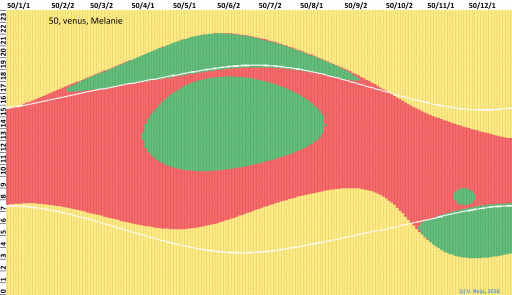
Venus without influence of Moon light (using Schaefer)
References
Blackwell, R.H. 1946. 'Contrast thresholds of the human eye',
Journal of the Optical Society of America, Vol 36: pp. 624-43.
Carr, C. Jelleff, and Fisher Kenneth D., 'A study of individual
variability in dark adaptation and night vision in man'. Washington:
Life sciences division. Army research office, 1970.
Evans, James, The history and practice of ancient astronomy: Oxford
University Press, USA, 1998.
Hecht, S. 1947. 'Visual threshold of steady point sources of light
in fields of brightness from dark to daylight', Journal of Optical
Society of America, Vol 37: p 59.
Inklaar, Frank. 1989. 'Een nieuwe methode voor de berekening van
heliakische opkomsten', University of Amsterdam. Download
the Dutch thesis, with permission of Frank Inklaar
Jong, Teije de. 2006. "The heliacal rising of Sirius." in Ancient
Egyptian chronology, ed. by E. Horning, Rolf Krauss and D.A.
Warburton, Vol 83: pp. 432-38. Leiden: Brill.
Jong, Teije de. 2012. 'Babylonian observations of Venus: Arcus
Visionis, atmospheric extinction an observation practice', Journal
for the History of Astronomy, Vol xliii: pp. 391-409.
Koch, Dieter. 2013. "Swiss Ephemeris." ed. by Alois Treindl.
AstroDienst. in http://www.astro.com/swisseph/.
Kolev, Rumen K., The Balylonian astrolabe: The calendar of creation,
The Neo-Assyrian text corpus project, Vol. XXII, 2013.
Krauss, Rolf, and Victor Reijs. 2012. "Babylonian crescent
observation and Ptolemaic-Roman lunar dates." in PalArch’s Journal
of Archaeology of Egypt/Egyptology, Vol 9,. in
http://www.palarch.nl/wp-content/Krauss-2012.-Babylonian-Crescent-Observation-and-Ptolemaic-Roman-Lunar-Dates.-PJAEE-9-5.pdf.
Krisciunas, K., and Brad E. Schaefer. 1991. 'A model of the
brightness of moonlight', Astronomical Society of the Pacific, Vol
103: pp. 1033-39.
Morrison, L.V. Stephenson, F.R., “Secular and Decade Fluctuations in
the Earth’s Rotation: 700 BC - AD 1978”, in: W. Fricke & G.
Teleki (eds.), Sun and Planetary System. Reidel Publ. Co.,
Dordrecht, 1982, pp. 173-178.
Morrison, L.V., and F. Richard Stephenson. 2004. 'Historical values
of the Earth's clock error Delta T and the calculation of eclipses',
Journal for the History of Astronomy, Vol 35: pp. 327-36.
Neugebauer, Otto, History of ancient mathematical astronomy, Volume
II, New York: Springer Science, 1975.
Pachner, Norbert. 2010. 'Am Rande der Nacht: Sichtbarkeitsperioden
von Gestirnen', Der Sternenbote.
Ptolemy, Claudius, Ptolemy's Almagest. Translated by G.J. Toomer:
Springer-Verlag, 1984.
Reijs, Victor M.M. 2012.'ARCHAEOCOSMO', in
http://www.archaeocosmology.org/eng/archaeocosmoprocedures.htm
[accessed 5 July 2012].
Rozenberg, Georgiĭ Vladimirovich. 1966. Twilight: a study in
atmospheric optics (New York: Plenum Press).
Schaefer, Brad E. 1985. 'Predicting heliacal rising and settings',
Vol 70: p 261.
Schaefer, Brad E. 1993. 'Astronomy and the limits of vision',
Archaeoastronomy: The journal of astronomy in culture, Vol XI: pp.
78-91.
Schaefer, Brad E. 1989. 'Refraction by Earth's atmosphere', Sky and
Telescope, Vol 77: pp. 311-13.
Schaefer, Brad E. 1998. "VISLIMIT.BAS." Version: Bugfixes by Victor Reijs. Sky and
Telescope. in
https://skyandtelescope.org/astronomy-resources/basic-programs-from-sky-telescope/
Schaefer, Brad E. 2000. 'New methods and techniques for historical
astronomy and archaeoastronomy ', Archaeoastronomy: The journal of
astronomy in culture, Vol XV: pp. 121-35.
Schoch, Carl. 1924. 'The 'Arcus Visionis' of the planets in the
Babylonian observations', Monthly Notices of the Royal Astronomical
Society, Vol 84: pp. 731-34.
Acknowledgements
I would like to thank people, such as Rob van Gent, Frank
Inklaar, Teije de Jong, Frank Prendergast, Rolf Krauss, Norbert
Pachner and Georg Zotti for their help and constructive feedback.
Any remaining errors in methodology or results are my
responsibility of course!!! If you want to provide constructive
feedback, let me
know.
Disclaimer
and Copyright
 Home
Home Up
Up Search
Search Mail
Mail
Major content related changes: Oct. 27, 2016