 Home
Home Up
Up Search
Search Mail
Mail
NEW
Lunar declination and azimuth
The lunar declination (and thus its azimuth) is determined by many aspects:
- the ecliptic (with a constant influence of obliquity on
declination of 23.44°, at 2000 CE)
- the lunar inclination (with a maximum influence on declination
of 5.1454°, the maximum is independent on the epoch, the actual
value is depending on the nodal cycle)
- the perturbation in the lunar inclination (depending on the
relative position of sun and moon, with a maximum of 8.7' or
-10').
- the parallactic fluctuation (amounting to 6' over a 180 Year
period: Ruggles [1999]).
- others (hopefully these have a smaller contribution than 1')
Remember that the error in the moon's position around 4000 BCE is around 13', so influences smaller
than 1' are not important.
The relative effects of the first three can be calculated
independently, but the overall effect is a combination of:
- the positions of moon and sun (determining the perturbation),
- the position of the lunar nodes with
respect to the solar vernal/autumnal points and
- lunar parallax
Perturbation of the lunar
inclination
Introduction
This section only talks about the perturbation of the lunar
inclination (which has a micro effect on the actual moon
declination), remember that the moon's path is also determined by it
normal changing inclination.
Theory
A formula for the perturbation of the lunar inclination is given by
L.V. Morrison ([1980] and pers.
comm. [2001]):
Perturbation = 8.65cos(2Lsl) - 0.70cos(2(Lml-L
sl))+ 0.65cos(2Lml) [']
Lsl: Sun's longitude measured from the longitude of
the lunar node
Lml: Moon's longitude measured from the longitude of
the lunar node
Remark: North [1996,
page
563] made a mistake by talking
about the ecliptic longitude of sun and moon. Luckily
this error does not really effect the rest of the points North
makes.
Remark: A. Thom
and A.S. Thom [1978] copied an
erroneous formula from M. A. Danby [1962] (the second argument
had a + instead of a -), which changes the big wobble values to
resp. +10' and -8.7' instead of +8.7'
and -10'. Due to this Thom used an
inclination between 5° 18' 43" and 5° 0' 1", while it should
have been: 5°17' 25" and 4° 58' 43". If this causes problems to
Thom's high precision deductions, I don't know.
If we graph this formula, we get the following:
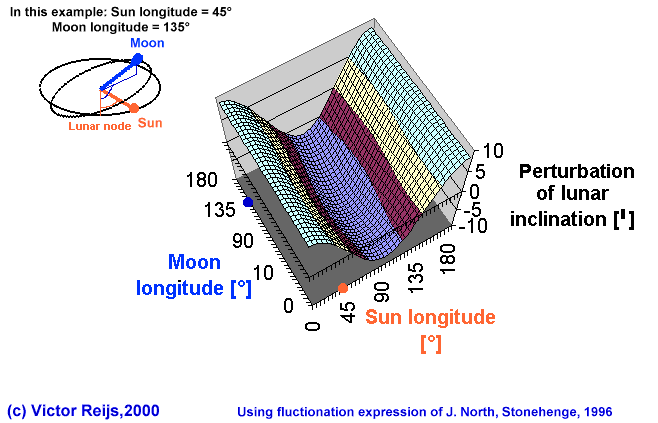
(the graph repeats itself after 180° solar longitude and after
180° lunar longitude)
Important solar and lunar events:
- First and last quarter moon
90° or 270° difference between solar and lunar longitude
- New moon
0° difference between solar and lunar longitude
- Full moon
180° difference between solar and lunar longitude
- Possibility of eclipses
If the Sun is inline with the lunar nodes (Ls1 of 0° or
180°), which is at the maximum of the perturbation, and if new or
full Moon there is a possibility of an eclipse
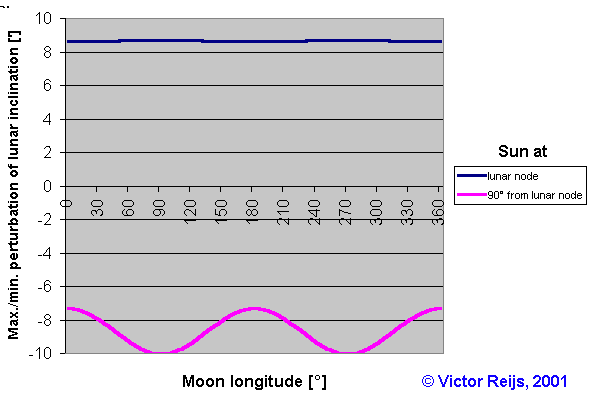
Different variations can be noticed in the moon's perturbation:
- Any lunar phase around the major/minor standstill limits and
any location of the sun.
A variation in perturbation of some 19': from +8.7' to -10' (big
wobble)
- Lunar phases around moment that the sun is near lunar nodes
The variations in perturbation are so small (around 0.1') that
they are not noticeable without modern tools.
Remember that a change in air pressure of 8 mbar already provides
the same change.
- Lunar phases around moment that the sun is 90° from the lunar
nodes
The variations in perturbation are so small (around 2.6') that
they are not noticeable without modern tools.
Remark: This is different from what North [1996, page 564] is telling in his
text, but not in his pictures.
Remark: A.
Thom [1973] copied an erroneous
formula from M. A. Danby [1962] (the second argument had a +
instead of a -), which might have shown him that full/new Moons
would have the maximum declination (the pink line would have been
around +10'). As can be seen, the quite stable blue line is on top
(at around +8.7'), but slightly peaking at quarter-ish moons.
Conclusion on perturbation
One can use all the moon phases around a standstill limit, because
there are no decernable differences between the inclination at any
of the moon phases. The largest perturbation difference is seen
between the sun near a lunar node and the sun at 90° from a lunar
node (with a period of ~ 0.5 ecliptic year ~173.31 Days and maxima
at quarter lunar phases and minima at full/new lunar phases).
Standstill limits due to the lunar
nodal cycle
The major standstill limit of the moon can be reached if the lunar
node is near the vernal (or autumnal) point, and thus the Moon has
its max. distance from the equator, equal to a declination at
present days of 23.44° + 5.1454°= 28.59°.
The minor standstill limit of the moon can be reached if the lunar
node is near the vernal (or autumnal) point, and thus the Moon has
its min. distance from the equator, equal to a declination at
present days of 23.44°- 5.1454° = 18.29°.
Declination of moon
When combining the effects of the lunar
nodal cycle and the perturbations we get the following theoretical
geocentric major and minor standstills limits:
- theoretical major standstill limit
This will happen at the moment the moon is near a quarter moon and
the lunar node is near the vernal (or autumnal) point. The moon is
at his highest point in its orbit and combining this with lunar
phase, the sun is near equinox.
The (geocentric) declinations of the theoretical major standstill
limits at present days are 28.59° + 0.145° = 28.74° (or
-28.74°)
- theoretical minor standstill limit
This will happen at the moment the moon is near a full/new moon
and the lunar node is near the vernal (or autumnal) point. The
moon is at his lowest point in its orbit and combining this with
lunar phase, the sun is near solstice.
The (geocentric) declinations of the theoretical minor standstill
limits at present days are 18.29°- 0.145° = 18.14° (or
-18.14°)
Lunar parallax
The lunar parallax comes into play, because we are observing the
moon rises and sets (see below): topocentric declinations. The mean
horizontal parallax changes the apparent altitude of the moon,
because we are not observing the moon from the center of the earth
(max: 60'.24 and min. 53'.97). This topocentric altitude makes that
the moon appears lower in the sky and thus the rise and set azimuths
of the moon will be more southern.
The most important though for this discussion is that the parallax
is also dependent on the distance between earth and moon, so the
lunar parallax and thus the moon set and rise azimuths are also
dependent on the anomalistic month.
Azimuth of moon
Calculating the resulting azimuth of the moon as a function of the
days after a major standstill limit (one can see here only the
maximum reachable values of the moon's azimuth and not the actual
values):
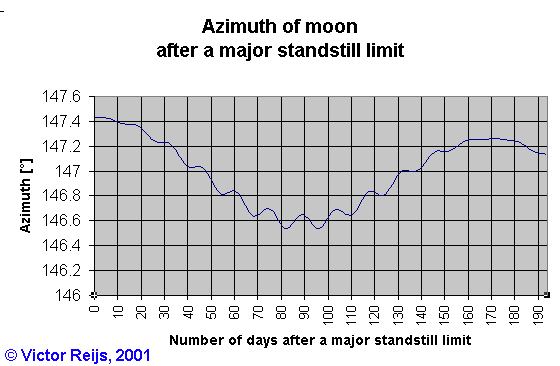
There is a difference in the major/minor
standstill limits in declination (which is the definition of major
standstill limit) and the method I am using; which is the apparent
major/minor azimuth standstill limit. This is because the
rise/set moments of the moon do not necessarily have to be the
same moments as reaching the extreme declination as seen in the
below picture. Also different locations may experience different
dates for the apparent major/minor azimuth standstill
limits.
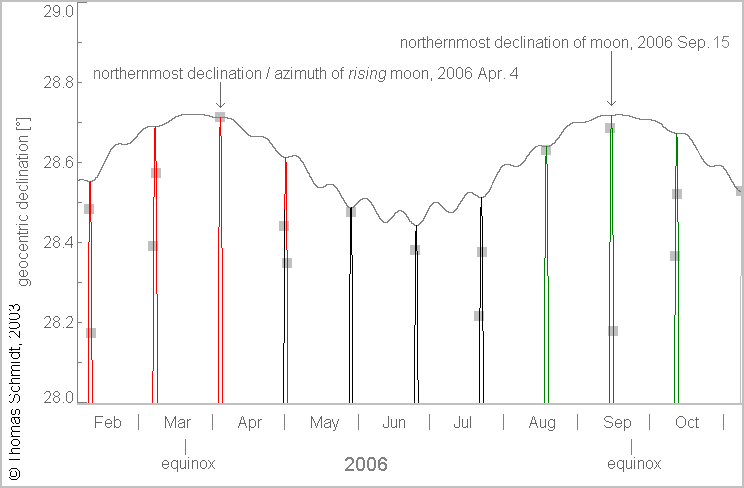
The grey squares are the lunar set and rise events.
The above picture has been made by Thomas
Schmidt
These can differ by a few periods of the tropical month!
On my web-site I use the following convention: When I talk
about major standstill limit it is always in the standard
definition, thus looking at declination, and if I use 'major/minor
azimuth standstill', I am looking at the real or apparent
extremes in azimuth.
Using the azimuth is perhaps more relevant for this web site,
because I think that that azimuth value could have been observable
by Neolithic man and not the (modern grid of the) declination.
The following can be deducted from all the above:
- The big wobble is due to the 9' declination wobble of the
perturbation of the moon's inclination. The maximum of this
wobble is at a first/third quarter moon and the minimum is at a
new/full moon. The period is ~ 0.5 ecliptic year or ~173.31
Days.
I have the opinion that a difference of some 0.9° is measurable
with a megalithic building. According to Thom [1973] megalithic people did, according
to Ruggles [1999] this can't be
proven (yet?).
- Megalithic buildings were perhaps able to registrate this
observed difference (0.9°) between moon's azimuth or a way to predict eclipses (like said by Thom [1973, page 19])
- The small wobbles (0.1' and 2.6') are due to the changing
positions of moon and sun (resulting in different phases of the
moon). The small wobbles are too small to be measured by means
of megalithic buildings.
- If the big wobble would not be there,
the experienced periodicity of the minor/major azimuth
standstill limits would be ~18.61 Years (lunar nodal cycle). Due
to the big wobble, the experienced periodicity of the
minor/major azimuth standstill limits is clustered around ~18,
~18.5 and ~19 years (due to the periodicity of the wobble of
half an eclipse year).
If one only looks at rises/sets of the moon during day time or
night time, it changes to a ~18 and ~19 year periodicity.
In the below picture this can be seen for the moon rises
calculated using JPL and gathered by
Jo Coffey over a 180 year period. Dates are Julian dates (that is
why they look out of date with equinox, but they are not).
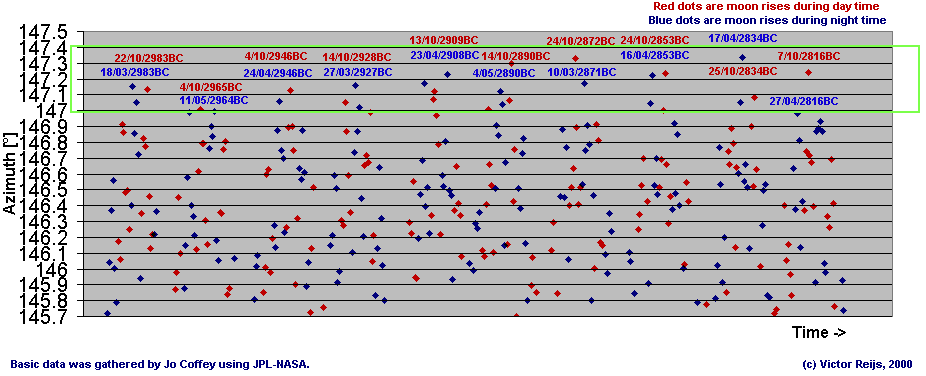
While checking this period for major
azimuth standstill limits and the following periods can be seen
(green for a time difference very
close to 19 tropical years [Metonic cycle] and purple for a time difference close to
18.03 tropical year [Saros cycle]):
- Day and night rising times:
18.5 - 19 - 18.5 - 19 - 18.5 - 18
- 19 - 18.5 - 18.5
- Day rising times:
18 - 19 - 18-
19 - 19
- 18 - 19
- 19 - 18
- Night rising times (most likely witnessed):
19 - 18 - 19 - 19 - 18 - 19 - 18 -
19 - 18
The distribution of Saros and Metonic cycles within the series is
quiet interesting!
Because the set and rise azimuth of the moon is dependent on the
tropical year, nodal cycle, synodical, anomalistic and draconic
month, it is expected that the total azimuth shows Metonic cycles (depending on
tropical years and synodical months) and Saros cycles (depending on
synodical, anomalistic and draconic months).
- It is perhaps interesting to see that such a sequence of
periods was also proposed by Hawkins to explain his 'computer'
at Stonehenge (see e.g Brown [1978],
page 125). I wonder if the sequence Hawkins has proposed, has
ever been related to this manifestation of the lunar nodal
cycle?
- Perhaps this 18 - (18.5 -) 19 year wobble in time has been
more easily observed, than the 0.9° wobble in azimuth?
- The question arises if an accurate
determination of the real major/minor azimuth standstill limit date
within the 18 - (18.5 -) 19 year wobble can be determined using
a passage cairn or free standing stones.
For determining the real date of azimuth standstill limit, there
is a window of some 0.4° azimuth in which the minor/major azimuth
standstill limit for that 18.61 Year period will occur (between
147° and 147.4°, see above picture).
But the accuracy is not that big, because the boundaries between
max. light intensity of the moon light patch and real shadow is
quiet faint. This is also due to size of quarter moon, also some
0.25°, which is in the same order as the difference we want to
measure. With a 12 m passage this is some 5 cm change in
shadow on a back wall (if you use the passage walls, this 5 cm
will of course grow to bigger figures,
so the faint difference between moon light and darkness will make
it less accurate). Remember that the standstill limit does not
have to be at the same moment as set or rise, this will also
introduce a small error (around 0.1°). The variation of altitude
due to astronomical refraction (0.07°) and parallax (0.1°) could
also make things less accurate (this results in a variation of
azimuth of 4 times bigger).
So determining the real date and thus the periodicy (of
18, 18.5 and 19 years) of major/minor azimuth standstill limits
will not be that simple using shadows on a passage (back-)wall.
- A comparison
of calculations is done of major azimuth standstill dates.
This also stresses the idea that one date for the major azimuth
standstill limit is not practical. This idea is also mentioned
by Thom ([1973], page 18):
"The Moon, it is true, in no sense stands still, but for about
a year the limiting declinations do not vary more than 20 arc
minutes, so that for month after month the Moon's declination
goes through almost the same cycle."
Acknowledgments
Thanks to the phenomenological work of Jo Coffey (except
that the actual major azimuth standstill limit dates mentioned [in
BCE and CE periods] are wrong but she is working on this; the form
of the graphs though are oke) and the help of Leslie Morrison and
Thomas Schmidt, I was stimulated to make this theoretical page.
Another very related page is on the Hopewell
lunar
astronomy (except that in this page in most instances draconic
month has to be replaced with tropical month).
Disclaimer and Copyright
 Home
Home Up
Up Search
Search Mail
Mail
Last major content related changes: April 7, 2001



